Voorbeeld van de klassieke berekening van een kistdam - Bijlagen

Waterspanningen

Het waterspanningsverloop is geschematiseerd zoals aangegeven in figuur 1.

Figuur 1 Waterspanningsverloop over de diepte

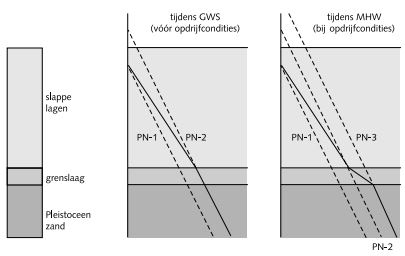
Verkeersbelasting

In dit voorbeeld is rekening gehouden met een verkeersbelasting van 13 kN/m2 tussen de kistdammen met een breedte van 2,5 m grenzend aan de polderwand.

Kistdamgegevens

De damwanden die in de berekeningen gebruikt zijn hebben de volgende eigenschappen (rekenwaarden):

Tabel 4 Rekenwaarden voor damwand- en ankergegevens

Bepaling inheidiepte damwanden volgens Blum en Homberg

Volgens Methode Blum wordt de lengte van de polderwand bepaald. Hierbij wordt ervan uitgegaan dat voor de polderwand volledige inklemming in de grond bereikt wordt. Dit levert een lengte van de polderwand en een ankerkracht op. Vervolgens wordt met de Methode Homberg de gereduceerde passieve drukverdeling tegen de rivierwand bepaald, waarmee de benodigde lengte van de rivierwand bekend wordt.

De resultaten zijn als volgt:

Tabel 5 Inheidiepte polder- en rivierwand volgens Homberg

Uitgangspunten

Aangezien in de beschouwde situatie de opdrijfveiligheid groter dan 1,2 is, is de overall stabiliteit met de Methode Bishop onderzocht. Voor de berekening van de overall stabi- liteit van de dijk is gebruik gemaakt van computerprogramma MSTAB, gebaseerd op de Methode Bishop.

Voor wat betreft het waterspanningsverloop is uitgegaan van het volgende:1)

• Het freatisch vlak verloopt van NAP +2,0m in de kruin van de dijk, naar NAP -1,3m in de polder.
• In het dijksmateriaal heerst een waterdruk die hydrostatisch verloopt met de diepte ten opzichte van het freatisch vlak.
• In het slappe lagenpakket heerst een waterdruk die lineair verloopt in de diepte tussen het freatisch vlak in het dijksmateriaal en de stijghoogte in het Pleistoceen zand onder gemiddelde omstandigheden, te weten NAP -0,5m.
• In het diepe zand heerst een waterdruk die hydrostatisch verloopt met de diepte ten opzichte van gemiddelde omstandigheden.

Zie voor de schematisatie van de waterspanningen figuur 1, het waterspanningsverloop tijdens GWS.

Berekeningsresultaten

De Bishop berekening leverde het volgende resultaat voor cirkels onder de constructie door:

Tabel 6 Stabiliteit volgens Bishop; geval 1

Uit de resultaten blijkt dat de overall stabiliteit van de kistdamconstructie voor het geval zonder overdruk in het pleistocene zand voldoet aan de norm van 1,17. Het mecha- nisme overall stabiliteit is dus niet maatgevend.

Horizontaal evenwicht

Het horizontaal evenwicht van de kistdamconstructie is bepaald zoals aangegeven in paragraaf 5.2.8. Hierbij is aangenomen dat de passieve kracht volledig tot ontwikkeling komt.

De berekening van het horizontaal evenwicht geschiedt met rekenwaarden voor de parameters en de veiligheid staat in tabel 7 gerangschikt.

• Deze aanname van het waterspanningsverloop wijkt af van de in het Voorschrift Toetsen op Veiligheid en bijlage A voorgestelde methode. Uit dit overzicht volgt dat voor een inheiniveau van NAP -12,5m aan de norm voor horizontaal evenwicht wordt voldaan.

Inwendig evenwicht

Het inwendig evenwicht van de vulling van de kistdamconstructie is bepaald zoals aangegeven in paragraaf 5.2.6

Tabel 8 Veiligheid tegen afschuiven van de vulling van de kistdam

Uit de tabel volgt dat bij een inheiniveau van NAP -15m het inwendige evenwicht aan de eis van 1,17 voldoet.

Bij de berekening van het inwendig evenwicht volgens Terzaghi wordt ervan uitgegaan dat actieve en passieve gronddrukken volledig tot ontwikkeling komen. Bij langere damwanden zal het uitwendig moment op de kistdamconstructie toenemen door toename van de actieve en passieve krachten en door toename van de arm.

In tabel 8 is derhalve zichtbaar dat wanneer de lengte van de damwanden wordt vergroot, de veiligheid tegen afschuiven van de vulling van de kistdam eerst afneemt en pas toeneemt wanneer de damwanden tot enkele meters in het pleistocene zand worden doorgezet. Dit wijst erop dat verlengen van de damwanden tot grotere verplaatsingen aan de top van de polderwand kunnen leiden.