Ontwerp volgens de klassieke methode - Veiligheidsbenadering ten aanzien van ontwerp en toetsing

Klassieke berekeningsmethode voor kistdam en diepwand

De klassieke berekeningsmethode is een verzameling van rekenmodellen gebaseerd op klassieke theorieën en modellen (zie hoofdstuk 5). Elk bezwijkmechanisme wordt apart met een eigen rekenmodel berekend. Hierbij wordt een deterministische (of semi- probabilistische) veiligheidsbenadering gehanteerd.

Bij toepassing van klassieke rekenmodellen kan de benodigde veiligheid worden gereali- seerd door toepassing van de juiste partiële materiaal- en belastingfactoren. In [38] is een methodiek aangegeven om de benodigde partiële factoren af te leiden. Deze methodiek volgt de lijn van Eurocode 1 (ENV 1991-1:1994, appendix A3). In de in [38] voorgestelde methode worden correctiefactoren toegepast op de materiaalfactoren uit de NEN 6700-serie en op de belastingfactoren uit NEN 6702. Onderstaand is deze methode kort toegelicht.

materiaalfactoren

De partiële materiaalfactoren, toe te passen op karakteristieke waarden (5% onder- grens), kunnen voor een lognormaal2 verdeelde sterkteparameter worden berekend met:

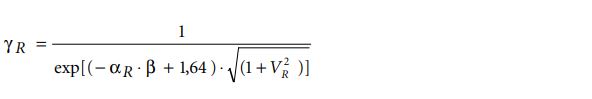
waarin:

γR        = materiaalfactor [-]

VR        = variatiecoëfficiënt [-]

αR        = invloedsfactor sterkte = 0,8 [-]

β          = betrouwbaarheidsindex [-]

De NEN 6700-serie gaat uit van materiaalfactoren, toe te passen op karakteristieke waarden (5%-ondergrens). Voor β= 3,6 zouden er in feite dan de waarden van de materiaalfactoren van de NEN 6700-serie gevonden moeten worden. Dit blijkt niet altijd het geval te zijn. Een en ander houdt verband met het voorkomen van trendbreuk.

Er wordt voor gekozen om de materiaalfactoren uit de NEN 6700-serie aan te houden, met dien verstande dat bij β > 3,6 er een correctiefactor fβ op de materiaalfactoren van de NEN 6700-serie wordt toegepast. Deze correctiefactor kan voor de uiterste grenstoe- standen worden berekend door met bovenstaande formule γR , te berekenen voor de vereiste β en voor β= 3,6. Het quotiënt hiervan levert de toe passen correctiefactor fβ:

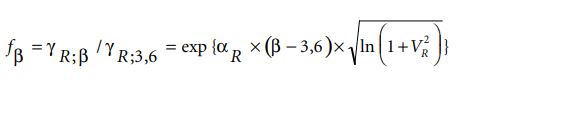
waarin:

fβ         = correctiefactor op materiaalfactoren volgens NEN 6700-serie [-]

γR;β     = materiaalfactor bij vereiste β[-]

γR;3,6  = materiaalfactor volgens NEN 6700-serie bij β= 3,6 [-]

Per parameter zijn met behulp van bovenstaande formule de volgende correctiefactoren voor de uiterste grenstoestand berekend.

Tabel 4.3 Correctiefactoren materiaalfactoren NEN 6700- serie uiterste grenstoestanden

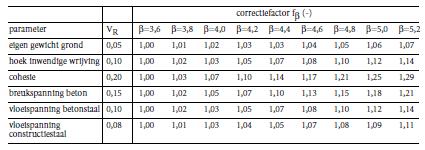
Opgemerkt wordt dat de waarden bij ‘eigen gewicht grond’ niet gelden voor grond als dood gewicht; in dat geval gelden de factoren van de NEN 6700-serie, te weten 0,9 á 1,0 voor gunstig werkende belastingen en 1,2 à 1,35 voor ongunstig werkende belastingen.

Voor de bruikbaarheidsgrenstoestand zou een analoge procedure kunnen worden gevolgd. Voor het bepalen van de correctiefactor fβ voor de bruikbaarheidstoestand moet dan in de formule in plaats van 3,6 de waarde 1,8 worden ingevuld. Veelal zullen echter voor de bruikbaarheidsgrenstoestand de partiële factoren op 1,0 worden gesteld.

De veiligheid volgt dan uit het gebruik van karakteristieke waarden en de streefwaarde van β= 1,8.

Hiermee wordt afgeweken van [39] omdat in genoemde bron ook voor de bruikbaar- heidsgrenstoestand met correctiefactoren wordt gewerkt (β > 1,8).