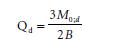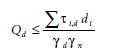Methode van Terzaghi - Rekenmodellen

Methode van Terzaghi

Voor de berekening van cellenkistdammen (zie paragraaf 2.1) wordt vaak gebruik gemaakt van de Methode van Terzaghi (1945). Daarbij wordt een model gehanteerd van langs elkaar schuivende verticale moten, zoals bij het omvallen van een serie tegen elkaar staande boeken. Dit komt overeen met het al eerder beschreven bezwijkmechanisme waarbij het grondlichaam in de kistdam niet vormvast is en het dwarsprofiel gaat vervormen tot een parallellogram (zie figuur 3.1a).

De Methode van Terzaghi beschouwt alleen de vormvastheid van de (cellen) kistdamconstructie. De methode bestaat uit de controle dat er geen afschuiving kan optreden langs het verticale middenvlak. Er wordt een lineaire verdeling verondersteld van de verticale druk op het funderingsvlak ten gevolge van het moment M0, dat veroorzaakt wordt door de uitwendige krachten ten opzichte van het midden van het grondvlak. Ten gevolge van de krachten W1, Fa en Fp wordt de kistdamconstructie belast met een moment. De door dit moment veroorzaakte schuifkracht moet kunnen worden opgenomen door de kern van de kistdam. De weerstand tegen afschuiven in het middenvlak moet groter zijn dan de schuifkracht in het middenvlak (zie figuur 5.3).

De toets op de vormvastheid van de kern van de kistdam is gebaseerd op Terzaghi. Hierin veroorzaakt het uitwendig moment een schuifkracht Q in de kern, volgens:

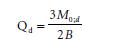
Deze schuifkracht moet worden opgenomen door de schuifsterkte van de afzonderlijke lagen:

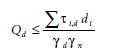
Waarin:

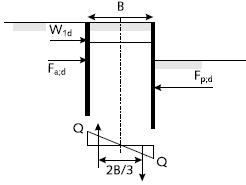
Het moment M0;d is de resultante van de momenten die de actieve en de passieve krachten ten opzichte van het schuifvlak onder beide damwanden op de kistdam uitoefenen, De arm is de afstand tussen het aangrijpingspunt van de passieve en actieve kracht en het schuifvlak aan de onderzijde van de kistdam.

Deze methode wordt in Nederland tot nu toe praktisch niet toegepast. In de Verenigde Staten wordt de methode vrijwel altijd gebruikt bij het ontwerpen van een cellen- kistdam.

Net als de hierna beschreven Methode Homberg is de Methode Terzaghi slechts een on- derdeel van de totale berekening. Het is dus niet een volledige toetsing van de grenstoe- stand van de kistdam. De methode gaat er voor de bepaling van het moment bovendien vanuit dat de vulling van de constructie zich gedraagt als een elastische vaste stof. Voor grond is dit een te simplistisch uitgangspunt, dat alleen geldt voor een zeer kleine hoekverdraaiing. Uit proeven is gebleken dat de aanname van een verticaal glijvlak in het midden van de kistdam niet correct is. Dit wordt ook bevestigd door waarnemingen verricht aan uitgevoerde constructies. Desondanks blijkt de Methode Terzaghi vaak voor de gebruikelijke kistdamconstructies (dus niet in dijken) in een goede eerste schatting van de benodigde afmetingen te resulteren. In [19] wordt op basis hiervan de volgende vuistregel gegeven:

1,5 H > B = 0,7 H

Hierin is B de onderlinge afstand van de twee damwanden en H de kerende hoogte. Wordt B > 1,5 H dan is er niet meer sprake van een kistdam.