Klassieke berekeningsmethode voor kistdam en diepwand - Ontwerpprocedure stap voor stap

Klassieke berekeningsmethode voor kistdam en diepwand

De klassieke berekeningsmethode is een verzameling van rekenmodellen gebaseerd op klassieke theorieën. Elk bezwijkmechanisme wordt apart met een eigen rekenmodel berekend. Voor een voorbeeldberekening wordt verwezen naar bijlage B en C. Er wordt getoetst aan een stabiliteitseis en een vervormingseis. De stappen van de klassieke berekening zijn:

Voorbereiding

1. Kies globale afmetingen voor de over het hele traject toe te passen kistdamcon- structie: inheidiepte van de wanden en afstand tussen de wanden, door voor onder- staande mechanismen afzonderlijk berekeningen uit te voeren.

2. Stel rekenwaarden vast voor de eigenschappen van grond en constructie-elementen door toepassing van de partiële factoren voor de uiterste grenstoestand op karakteristieke schattingen van de gemiddelde waarden.

3. Stel waterstanden en waterspanningen vast die gelden voor de uiterste grenstoestand.

Voer voor elk representatief dwarsprofiel de volgende berekeningen uit:

Uiterste grenstoestand (zie figuur 8.2)

1. Beschouw de stabiliteit van het grondlichaam naast de kistdam of diepwand:

   • indien de opdrijfveiligheid kleiner is dan 1,2: stabiliteitsberekeningen volgens het drukstaafmodel en waterspanningen behorend bij de uiterste grenstoestand;

   • indien de opdrijfveiligheid groter of gelijk is dan 1,2: stabiliteitsberekeningen volgens Bishop met gedraineerde sterkteparameters en waterspanningen behorend bij de uiterste grenstoestand.

2. Indien de stabiliteit van het grondlichaam naast de kistdam of diepwand onvol- doende is, modelleer dan een afgeschoven profiel op basis van het maatgevende bezwijkmechanisme uit de vorige stap. Hierbij zal de aandrijvende grondmassa zakken en de weerstandbiedende grondmassa omhoog komen. Het volume van de afzonderlijke grondlagen in het afgeschoven deel verandert niet ten opzichte van de oorspronkelijke situatie. Ook de diepte van de freatische lijnen in het afgeschoven deel verandert niet.

3. Indien de opdrijfveiligheid kleiner is dan 1,2: bereken de overall-stabiliteit inclusief kistdam of diepwand volgens het drukstaafmodel met waterspanningen behorend bij de uiterste grenstoestand.

4. Indien de opdrijfveiligheid groter of gelijk is dan 1,2: berekende overall-stabiliteit inclusief kistdam of diepwand volgens Bishop met gedraineerde sterkteparameters en waterspanningen behorend bij de uiterste grenstoestand.

5. Pas op basis van bovengenoemde stabiliteitsberekeningen de afmetingen van de damwanden zodanig aan dat de vereiste veiligheid wordt bereikt.

   

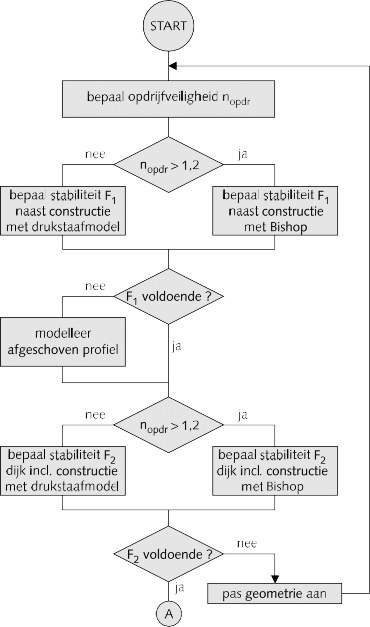
   Figuur 8.2 Stroomschema klassieke berekening

   Stap 6 t/m 12 voor kistdam

6. Bepaal de minimaal benodigde inheidiepte van de polderwand met Methode Blum, de ankerkracht is hiermee bekend.

7. Controleer of de passief benodigde kracht uit de damwandberekening (bijvoorbeeld Methode Blum) kleiner is dan de maximaal mobiliseerbare kracht in de passieve grondmassa. Dit is nodig omdat in de berekening geen rekening wordt gehouden met de reductie van de schuifspanning die kan worden afgedragen aan de draag- krachtige laag in situaties van opdrijven van het voor- of achterland. De maximaal mobiliseerbare passieve kracht ter plaatse van de kistdam volgt uit figuur 8.2.

   

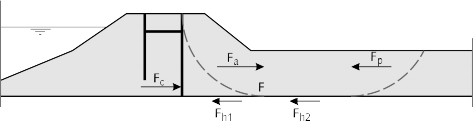
   Figuur 8.3 Horizontale krachten buiten de constructie vóór en na opdrijven

   waarin:

   Fc      = kracht uitgeoefend door kistdam [kN/m]

   Fa      = actieve kracht van talud op achterland [kN/m]

   Fp      = passieve weerstandbiedende kracht in achterland [kN/m]

   Fh1    = weerstandbiedende kracht langs draagkrachtige laag, onder talud [kN/m]

   Fh2    = weerstandbiedende kracht langs draagkrachtige laag, onder achterland [kN/m]

   In het algemene geval geldt:

   Fc;max = Fa + Fh1

   Hierbij dient Fh1 te worden bepaald bij maatgevend hoogwater. In dat geval veroor- zaakt de kracht Fc;max die maximaal door de kistdam op het achterland wordt uitge- oefend geen extra vervormingen in het achterland, buiten de vervormingen die toch al zouden optreden ten gevolge van het opdrijven van het achterland. De kracht Fc;max , wordt bepaald met de maximale waarde van Fa. Meestal is Fa maximaal in een verticaal gelegen bij de teen van het achtertalud. Voor het geval dat de stabiliteit van het grondlichaam buiten de constructie voldoende is, is de kracht Fa een actieve kracht en vormt daarmee een ondergrens voor de ter plaatse optredende kracht.

   Hieruit volgt dat de kracht Fc;max ook een ondergrens is. Dit betekent dat als de kistdam met klassieke rekenmodellen met in acht name van de kracht Fc;max wordt ontworpen ter plaatse van de kistdam in principe geen extra vervormingen als gevolg van het opdrijfmechanisme zullen optreden.

   Als de stabiliteit van het grondlichaam buiten de constructie onvoldoende is en het binnentalud inzakt geldt:

   Fa = Fh2 + Fp

8. zodat:

   Fc;max = Fh1 + Fh2 + Fp

   Maatgevend voor de kracht Fc;max is in dit geval de verticaal waar de som van Fh2 en Fp, minimaal is. In dat geval zal voor Fa een grotere waarde worden gevonden dan het geval zal zijn als het binnentalud niet inzakt. Het hieraan ten grondslag liggende bezwijkmechanisme bevind zich echter volledig buiten de kistdam. Hieruit volgt dat ook in dit geval ter plaatse van de kistdam zelf geen extra vervormingen als gevolg van het opdrijfmechanisme zullen optreden.

   De berekening van de maximaal mobiliseerbare passieve kracht gebeurt het gemakkelijkst met behulp van een programma voor het uitvoeren van drukstaafbe- rekeningen, zoals MLIFT. Bij de berekeningen met MLIFT wordt geen rekening gehouden met vervormingen.

9. Indien de maximaal mobiliseerbare passieve kracht in de passieve grondmoot kleiner is dan de passieve kracht die nodig is volgens de damwandberekening, herhaal dan de damwandberekeningen met gereduceerde sterkteparameters. Doe dit totdat de benodigde kracht gelijk is aan de maximaal mobiliseerbare kracht.

10. Bereken de lengte van de rivierwand die wordt belast door de uitwendige belasting, de ankerkracht (uit de polderwand), en de passieve druk volgens de Methode Homberg.

11. Indien de verplaatsingen van polder- en rivierwand niet in overeenstemming zijn met de verlenging van het anker, bereken dan de polderwand opnieuw met aange- paste ankerstijfheid.

12. Toets of de staalvloeispanning in damwanden en ankers niet wordt overschreden; kies zonodig een ander damwandprofiel of ankerdoorsnede en herhaal de bereke- ningen met de Methode Blum en Homberg.

13. Toets of het inwendig evenwicht en het horizontaal evenwicht van de kistdam aan de eisen voldoen; breng hierbij de passieve kracht uit de Methode Blum, al dan niet met gereduceerde sterkteparameters, in rekening.

Stap 6 t/m 9 voor diepwand

1. Bepaal het minimaal benodigde teenniveau van de diepwand met de methode van de verend ondersteunde liggers.

2. Controleer of de passief benodigde kracht uit de vorige stap kleiner is dan de maximaal mobiliseerbare kracht in de passieve grondmassa. Dit is nodig omdat de methode van de verend ondersteunde liggers geen rekening houdt met de reductie van de schuifspanning die kan worden afgedragen aan de draagkrachtige laag in situaties van opdrijven van het voor- of achterland. De maximaal mobiliseerbare passieve kracht ter plaatse van de diepwand wordt op dezelfde wijze bepaald als in het geval van een kistdam.

3. Indien de maximaal mobiliseerbare passieve kracht in de passieve grondmoot kleiner is dan de passieve kracht die nodig is volgens de methode van de verend ondersteunde liggers, herhaal dan de berekeningen volgens de methode van de verend ondersteunde liggers met gereduceerde sterkteparameters. Doe dit totdat de benodigde kracht gelijk is aan de maximaal mobiliseerbare kracht.

4. Dimensioneer de wapening van de diepwand op de krachtsverdeling welke volgt uit de methode van de verend ondersteunde liggers. Als daarbij niet kan worden voldaan aan de eisen welke volgen uit de van toepassing zijnde betonvoorschriften pas dan het ontwerp aan.

N.B. Voor een diepwand zijn er geen stappen 10 t/m 12.

Bruikbaarheidsgrenstoestand voor kistdam en diepwand

13. Stel rekenwaarden vast voor de eigenschappen van grond en constructie-elementen door toepassing van de partiële factoren voor de bruikbaarheidsgrenstoestand op karakteristieke schattingen van de gemiddelde waarden.

14. Stel waterstanden en waterspanningen vast die gelden voor de bruikbaarheidsgrens- toestand.

Stap 15 voor kistdam:

15.Herhaal de berekeningen met de Methoden Blum en Homberg voor de bruikbaarheidsgrenstoestand en toets of de vervorming van de constructie aan de eis voldoet. Pas zonodig het ontwerp aan.

Stap 15 en 16 voor diepwand:

15. Verdeel, afhankelijk van het verloop van de in stap 9 bepaalde wapening, de diepwand over de hoogte in een aantal secties. Bepaal in overleg met een betoncon- structeur, rekening houdend met het M-κ diagram van de doorsnede, per sectie de buigstijfheid van de diepwand.

16. Herhaal de berekeningen met de methode van de verend ondersteunde liggers voor de bruikbaarheidsgrenstoestand en toets of de vervorming van de constructie aan de eis voldoet.

17. Pas zonodig in overleg met een betonconstructeur met behulp van de resulterende momentenverdeling de buigstijfheid per sectie aan.

Voor een diepwand geldt bovendien:

De afmetingen van de diepwand en de wapening worden in overleg met een betonconstructeur vastgesteld. Door het sterk variërende buigend moment over de hoogte van de diepwand is het meestal niet efficiënt om over de gehele lengte van de diepwand dezelfde wapening toe te passen. Als gevolg daarvan is de buigstijfheid over de hoogte meestal niet constant. Met M-κ-diagrammen kan voor iedere fase van de belasting voor iedere diepwandsectie een relatie worden bepaald tussen buigend moment en buigstijfheid. Ook kan de mogelijkheid van voorspannen van de diepwand worden overwogen. Bij een gelijke wanddikte resulteert dit in een grotere buigstijfheid die ook nog vrijwel constant is over de hoogte van de diepwand. Daardoor kan bij voorgespannen diepwanden vaak met een geringere wanddikte worden volstaan.

In de in [15] uitgevoerde berekeningen is als schatting gewerkt met 1/4 van de stijfheid van ongescheurd beton.

In paragraaf 8.6.3 van NEN 6720 is een ten opzichte van de methode met M-κ- diagrammen vereenvoudigde methode voor de bepaling van de gescheurde stijfheid van beton aangegeven.