Toelichting geostatistische berekening van sondeerafstanden - Bijlage D Toelichting geostatistische berekening van sondeerafstanden

In deze bijlage is een toelichting gegeven op de geostatistische berekening van de sondeerafstanden in Tabel 7 in de hoofdtekst.

We gaan uit van een patroon van variaties van de diepteligging van de onderkant van een klei/veenpakket (de laagscheiding met onderliggend zand) dat beschreven kan worden als een (normaal verdeelde) stationaire stochastische functie. Hiermee bedoelen we het volgende. Geven we de diepteligging van de laagscheiding aan met h(x), waarbij x de coördinaat is langs een horizontale as, dan is voor elke x de diepte h(x) een realisatie van de normaal verdeelde stochastische variabele h. De realisaties voor verschillende waarden van x, bijvoorbeeld x1en x2zijn meer of minder gecorreleerd, afhankelijk van de afstand 𝜏  tussen de punten x=x1en x=x2: τ = |x1- x2|. Hoe kleiner de afstand, hoe groter de correlatie. Voor grote afstand dempt de correlatie uit tot 0, dat betekent dus dat er geen correlatie is tussen de realisaties h(x1) en h(x2). De correlatie wordt beschreven door een zogenaamde autocorrelatiefunctie ρ(𝜏). Per definitie moet gelden: -1 ≤ ρ(𝜏) ≤ 1voor alle waarden van 𝜏. Noodzakelijk voor continuïteit (geen sprongsgewijze veranderingen) van het variatiepatroon is dat voor 𝜏→0 de correlatie  ρ(𝜏) tot 1 nadert. Doorgaans gaat men in de geostatistiek voor de beschrijving van een continu variatiepatroon uit van een autocorrelatiefuncie die de waarde 1 aanneemt voor 𝜏=0 en die geleidelijk afneemt naar 0 bij toenemende waarde van 𝜏. Voor een ‘glad’ verloop van het variatiepatroon (d.w.z. h(x) is differentieerbaar) is het nodig dat de eerste afgeleide van de auto- correlatiefunctie voor 𝜏=0 gelijk aan 0 is en continu is (geen sprong vertoont).

De parameters van de stochastische functie zijn:

• de verwachtingswaarde en standaardafwijking van de kansdichtheidsverdeling van h, deze geven we aan met µhen σh. In het rekenvoorbeeld in Tabel 7 in de hoofdtekst gaan we uit van een verwachtingswaarde van 10 m en een standaardafwijking van 1,20 m.

• de autocorrelatiefunctie. Hiervoor wordt veelal een exponentiële functie geko- zen, waarin de afstand 𝜏 in het kwadraat voorkomt. Als voorbeeld is gekozen:

D1)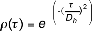

waarin Dheen autocorrelatieparameter is. Hoe kleiner Dh, hoe sneller het patroon van de opeenvolgende variaties (zie Figuur D 1).

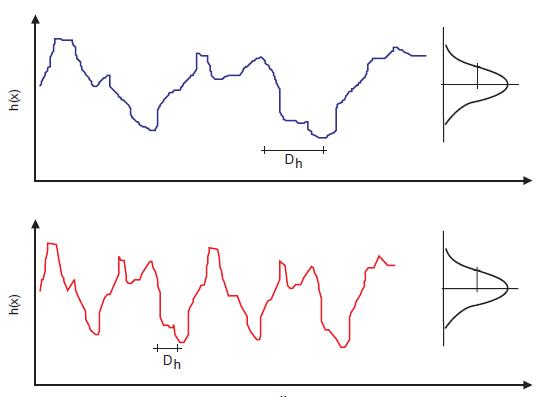
Figuur D 1

Variatiepatroon met grote autocorrelatieparameterDh(boven) en met kleine Dh(onder)

Een globale indicatie van de ‘correlatielengte’ Dhis 50 – 150 meter. Indien we beschikken over een voldoende gedetailleerde meting kunnen indicaties van Dh aan de meting zelf worden ontleend, met behulp van een variogram- of een correlatieanalyse; ook zijn soms vuistregels te geven van die parameter.

Met de verwachtingswaarde en de standaardafwijking kunnen we de kans bere- kenen dat op een willekeurige locatie binnen de dijkstrekking de diepteligging van de laagscheiding kleiner is dan 8 m ongeveer 5% is. Echter, de strekking in de lengterichting van de dijk is 2 km. Die strekking kan opgedeeld gedacht worden mootjes, waarvan de kansen op onderschrijden van de 8 metergrens steeds 5% zijn, maar de kansen voor de verschillende mootjes zijn onderling onafhankelijk. Bij een Dh van, bijvoorbeeld, 100 m zijn de lengtes van de ‘onafhankelijke’ mootjes bij benadering zo’n 130 m, er zijn dus grofweg 15 onafhankelijke mootjes. De kans dat er tenminste één mootje is waar de 8 metergrens wordt onderschreden is (uitgaande van de kans van 5% voor elk van de mootjes afzonderlijk):

D2)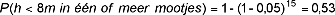

We kunnen ook zoeken naar de diepte, waarvoor de onderschrijdingskans voor alle mootjes samen 5% is. Dit noemen we de karakteristieke diepte, rekening houdend met het effect van ruimtelijke variatie. De onderschrijdingskans van elk afzonderlijk mootje moet dan 0,0035 zijn. Met de verwachtingswaarde µh= 10 m en de standaardafwijking σh=1,20 m vinden we dan een diepte van 6,75 m.

Stel nu dat we de diepteligging in de lengterichting van een dijktraject met behulp van sonderingen hebben gemeten, waarbij de onderlinge afstand tussen de son- deerpunten steeds gelijk is aan Δx. Stel verder dat de minimale gemeten diepte gevonden is in het punt x0en de bijbehorende diepte h(x0) is. Echter, tussen de

metingen zijn mogelijk nog kleinere diepten aanwezig. Hoeveel kleiner, hangt in belangrijke mate af van de afstand tussen de sondeerpunten Δx.

Met behulp van het boven besproken stochastische model kunnen een schatting maken van de mogelijke afwijking tussen de diepte in een punt waar gemeten is en punten tussen de meetpunten in. Statistisch is die mogelijke afwijking het grootst in het midden tussen twee meetpunten. De standaardafwijking van de mogelijke afwijking tussen de diepte op een afstand van Δx/2 van het punt x0 en de diepte in x0zelf berekenen we als volgt:

D3)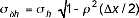

Hierin is σhde standaardafwijking van de diepteligging, die geschat kan worden uit de metingen en  ρ(Δx/2) de correlatie tussen een meetpunt en een punt midden tussen twee meetpunten. De conditionele verwachtingswaarde in dit punt, gegeven (alleen) de gevonden minimale waarneming h(x0) is:

D4)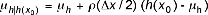

Met behulp van σδh en de conditionele verwachting µh|h(xo)kunnen we de kans berekenen dat de waarde van h in het midden van de sondeerintervallen links en rechts van x0een bepaalde gekozen kritieke waarde hcritonderschrijdt. Die kans is, uitgaande van een normale kansverdelingsfunctie van h:

D5)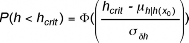

Hierin is Φ( ) de standaardnormale kansverdelingsfunctie.

In Tabel 7 van de hoofdtekst is, gegeven de aannames voor µh(10 m), σh(1,20 m) en Dh(respectievelijk 50, 100 en 150 m), voor enkele aangenomen waarden voor de minimaal gevonden diepte h(x0) (respectievelijk 8,5, 9 en 9,5 m) en een geko- zen criteriumwaarde waarde hcrit(8m), proberenderwijs gezocht naar sondeeraf- standen ∆x, waarbij de kans op onderschrijding volgens bovenstaande formule net 5% is. De hcritvan 8 m kunnen we dus opvatten als de karakteristieke 5% ondergrensschatting van h, gegeven de in de meting gevonden minimale dikte h(x0) en gegeven de afstand tussen de sondeerpunten.