Indien waarnemingsreeksen van parameters beschikbaar op grond waarvan representatieve waarden van parameters moeten worden bepaald, dan zijn de statistische procedures als volgt: gezocht worden schattingen van de parameters die slechts met een kans van 5% worden over- of onderschreden, de zogenaamde karakteristieke waarden. Onderscheid moet gemaakt worden naar de volgende situaties:
-
de waarnemingsreeks is een locaal of een regionaal gegevensbestand;
-
de gezochte karakteristieke waarde moet een representant zijn voor de individuele ‘punt’-waarde van de parameter of een representant voor de ‘laaggemiddelde’- waarde op de betreffende locatie waarvoor het mechanisme wordt onderzocht;
-
de waarnemingen kunnen worden opgevat als Normaal-verdeeld of als Log-Normaal- verdeeld.
Onder een locaal bestand van waarnemingen wordt verstaan een verzameling van waarnemingen die het resultaat zijn van grondonderzoek ter plaatse van de locatie waarvoor wordt getoetst. Onder een regionaal bestand wordt verstaan een verzameling van waarnemingen die het resultaat zijn van grondonderzoek over een veel groter gebied. Bedacht moet worden dat het gemiddelde van een regionaal waarnemingenbestand niet representatief behoeft te zijn voor het laaggemiddelde op een locatie; bij het vaststellen van karakteristieke parameterschattingen dient hiermee rekening te worden gehouden.
Zoals genoemd in paragraaf 4.3 van de hoofdtekst is voor sommige parameters in een rekenmodel de individuele ‘punt’-waarde van belang, voor andere het ‘laaggemiddelde’ op de locatie waarvoor de berekening moet worden gemaakt. Parameters in de pipinganalyse volgens de regel van Sellmeijer waarvoor de individuele puntwaarde van belang is zijn bijvoorbeeld de kwelweglengte en de dikte van de watervoerende zandlaag, voor zover die varieert in de langsrichting van de kering; van belang zijn de minimale kwelweglengte en de maximale dikte in de langsrichting van de kering. Voor de doorlatendheid van de zandlaag is daarentegen de laaggemiddelde waarde op een locatie van belang; variaties van ‘punt tot punt’ worden bij de grondwaterstroming min of meer ‘uitgemiddeld’.
Statistische procedures om op basis van een bestand van waarnemingen te komen tot karakteristieke schattingen, zijn gebaseerd op een aanname betreffende de kansverdeling van die waarnemingen. Veelal kan de Normale (Gausse) kansverdelingsfunctie worden verondersteld. Bij grote spreidingen in het waarnemingsmateriaal is het zinvol om een Log- Normale kansverdelingsfunctie te veronderstellen, omdat de aanname van een Normale kansverdeling daarbij kan leiden tot fysisch onrealistische karakteristieke waarden (bijvoorbeeld: negatieve karakteristieke waarde voor een parameter die per definitie een positieve waarde heeft).
Hieronder worden formules gegeven voor het berekenen van karakteristieke parameterschattingen (met 5% onder- of overschrijdingskans). We gaan uit van een waarnemingsreeks voor een parameter p, namelijk {p1, p2, …, pN}.
Bij een lokaal waarnemingsbestand:
Indien aangenomen wordt dat de waarnemingen normaal verdeeld zijn, luidt de formule voor karakteristieke schattingen voor individuele puntwaarden:
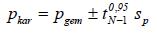 A(1.22)
A(1.22)
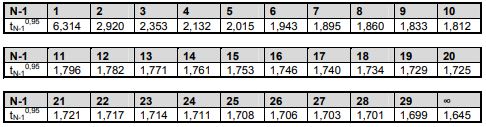
Hierin is pgem het rekenkundig gemiddelde van de waarnemingen, sp de standaardafwijking van de waarnemingen, N het aantal waarnemingen en tN-10,95 de Student-t factor. Met de laatste wordt verdisconteerd dat zowel het rekenkundige gemiddelde als de standaardafwijking slechts schatters zijn van de verwachtingswaarde en de standaardafwijking van de parameter. In onderstaande tabel zijn enkele t-waarden gegeven.
- Tabel B.2 t-waarden voor Student-t factor
De formule voor karakteristieke schatting van de laaggemiddelde waarde van p (uitgaande van een locaal waarnemingsbestand) luidt:
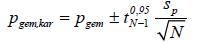 A(1.23)
A(1.23)
Het quotënt uit standaardafwijking sp en het rekenkundige gemiddelde van de waarnemingen pgem is de variatiecoëfficiënt Vc.
Bovenstaande vergelijking kan daarom ook worden uitgedrukt als:
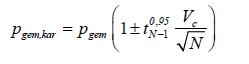 A(1.24)
A(1.24)
Indien de spreiding in de waarnemingsreeks groot is kan formule A(1.22) leiden tot onrealistische schattingen. In dat geval is het verstandig om een Log-Normale verdelingsfunctie te veronderstellen. De karakteristieke schatting voor individuele puntwaarden luidt dan:
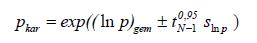 A(1.25)
A(1.25)
Hierin zijn (ln p)gemen sln p het rekenkundige gemiddelde en de standaardafwijking van de natuurlijke logaritmes van de waarnemingen.
De karakteristieke schatting voor een laaggemiddelde waarde is veelal minder gevoelig voor grote spreiding in de waarnemingen. We kunnen hiervoor formule A(1.23) blijven gebruiken. Echter, bij kleine aantallen waarnemingen kan dit toch problemen opleveren. In dat geval kan de volgende formule gebruikt worden:
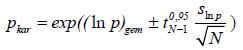 A(1.26)
A(1.26)
Bij een regionaal waarnemingsbestand:
Voor karakteristieke schattingen van ‘punt’-waarden maakt het geen verschil of het waarnemingsmateriaal uit locaal of regionaal grondonderzoek komt; voor deze schattingen kunnen de formules A(1.22) of A(1.25) worden gebruikt.
Voor karakteristieke schattingen van laaggemiddelde waarden voor de parameter moet, zoals gezegd, ermee rekening gehouden worden dat laaggemiddelden per locatie kunnen verschillen. Deze ruimtelijke variatie wordt verdisconteerd in de karakteristieke schatting:
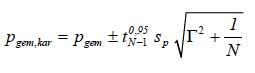 A(1.27)
A(1.27)
met Γ2 = 0,25 (zie [TAW, 1989]).

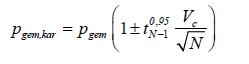 A(1.24)
A(1.24)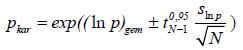 A(1.26)
A(1.26)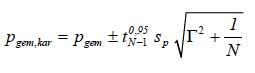 A(1.27)
A(1.27)