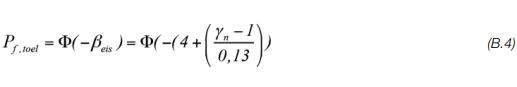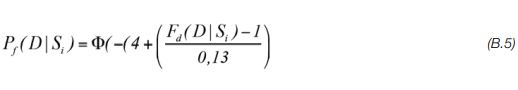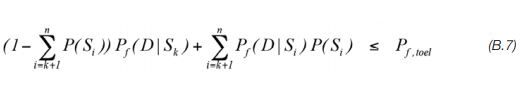Schematiseringtheorie; spreadsheetapplicatie macrostabiliteit - Theorie Schematiseringfactoren

Schematiseringtheorie; spreadsheetapplicatie macrostabiliteit

Voor een uitgebreide beschrijving van de theorie wordt verwezen naar het achter- grondrapport TRGS [24] of naar de SBW-onderzoeksrapportage [25]. Hieronder volgt een wiskundige beschrijving die de lezer in staat moet stellen het algoritme voor het bepalen van de schematiseringfactor in een spreadsheet of ander computer- programma te implementeren. We gaan er hier in eerste instantie van uit dat de analyse betrekking heeft op het faalmechanisme macro-instabiliteit van het binnen- talud van een dijk.

De verschillende mogelijke schematiseringen van de ondergrondopbouw en de waterspanningen voor een ontwerp- of toetsanalyse noteren we als de verzameling scenario’s {Si} (i=1…n). Een bestaande dijk of een ontwerp van een dijkversterking geven we symbolisch aan met D. De kansen dat de afzonderlijke scenario’s (het beste) de werkelijke ondergrondopbouw en waterspanningen onder en in dijk D in de toets- of ontwerpsituatie weergeven, geven we aan met P(Si) (i=1…n). We ver- onderstellen dat de werkelijke situatie door precies één van de scenario’s wordt weergegeven (de scenario’s sluiten elkaar dus onderling uit). De som van de kansen P(Si) (i=1…n) moet dus gelijk aan 1 zijn.

Uitgaande van elk van de scenario’s kunnen we, met behulp van hiervoor geschikte rekenmodellen, zoalsde Bishop glijcirkelanalyse of de Lift-Van analyse (bij opdrijven), een rij stabiliteitsfactoren van de dijk berekenen. Die rij noteren we als Fd(D⎪Si) (i=1…n). Dat zijn dus stabiliteitsfactoren van dijk D, uitgaande van de schematisering Si.

De veiligheidseis is gegeven in termen van een eis aan de stabiliteitsfactor. Voor een voldoend veilige dijk moet:

Hierin is Sween symbolische aanduiding voor de werkelijke ondergrondopbouw en hierin optreden waterspanningen, γn de zogenoemde schadefactor en γd de reken- modelonzekerheidsfactor (zie ook bijlage A). De rekenmodelonzekerheidsfactor voor de Bishop glijcirkelanalyse is gelijk aan 1.0, die voor de Lift-Van analyse is 1,05. Dit verschil kunnen we verdisconteren door de stabiliteitsfactoren die uit de Lift-Van analyse komen te delen door 1,05. We krijgen dan onderling vergelijkbare stabiliteitsfactoren en in vergelijking (B.1) is dan γd=1; waardoor we deze factor in het vervolg van de beschrijving weg kunnen laten.

De schadefactor is gerelateerd aan een probabilistische veiligheidsmaat via (zie het addendum bij het TRWG [4], of bijlage A):

Hierin is βeis de vereiste betrouwbaarheidsindex. Deze is gerelateerd aan een toelaatbare faalkans, via:

Hierin is Φ(.) de standaardnormale (Gausse) kansfunctie. Combinatie van (B.2) en (B.3) geeft:

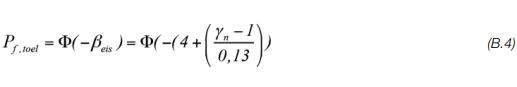
Met andere woorden, de eis in vergelijking (B.1) komt overeen met een eis aan de faalkans die gegeven wordt door vergelijking (B.4). De toelaatbare faalkans geeft de eis voor de constructie (de dijk) m.b.t. macrostabiliteit.

We kunnen de relatie (B.4) gebruiken als relatie om bij een stabiliteitsfactor de overeenkomstige (reken)faalkans te bepalen. Voor de rij stabiliteitsfactoren gegeven de scenario’s voor de schematiseringen {Si}:

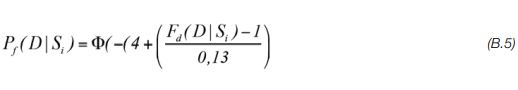
voor i=1…n. De totale faalkans is gelijk aan de som van de producten van de faalkansen bij elk van de mogelijke schematiseringen en de kansen dat die sche-matiseringen de werkelijkheid representeren. De eis (B.1) komt dus overeen met de volgende eis in termen van faalkansen, rekening houden met de onzekerheid over ondergrondopbouw en waterspanningen:

Veronderstel nu dat de nummering van de scenario’s zo gekozen is dat de bij-behorende rij stabiliteitsfactoren Fd(D⎪Si ) voor i=1,2,…n een dalende (althans niet stijgende) rij is, dan is de bijbehorende rij faalkansen Pf (D⎪Si ) een stijgende (althans niet dalende) rij. Door hernummering van de scenario’s is dat altijd moge-lijk. De verschillende scenario’s Si variëren dan in oplopende volgorde van i van opti-mistisch tot conservatief. Een van de scenario’s wordt gekozen als (althans in eerste instantie) basisschematisering; stel dat dit scenario Sk is, waarbij k groter dan 1 is en kleiner dan n. In de sommatie in vergelijking (B.6) zullen de grootste bijdragen aan de faalkans geleverd worden door de scenario’s met subscript i≥ k. We majo-reren de eis (B.6) daarom als volgt (de eis wordt daardoor iets strenger)

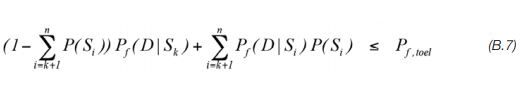
Het voordeel hiervan is dat we verder geen omkijken meer hebben naar de scenario’s die optimistischer zijn dan de basisschematisering, maar alleen naar de scenario’s die, als ze werkelijkheid zijn, een ongunstig effect op de stabiliteit hebben. Deze scenario’s vormen immers het risico, waar we ons tegen willen indekken. Wanneer we stabiliteitseis (B.1) zouden aanhouden voor de gekozen basisschematisering, dan staat niet op voorhand vast dat ook voldaan zou worden aan de eis (B.6). Sterker de kans is dan groot dat hier niet aan voldaan wordt. Immers de faalkansen bij de scenario’s Sk+1, Sk+2 , …Sn zijn groter dan(of tenminste gelijk aan)de faalkans bij basisschematisering (scenario Sk). Echter, of al dan niet voldaan wordt aan de eis (B.6) hangt af van de scenariokansen.

Als we een constructie kunnen bedenken waardoor aan de eis (B.7) wordt voldaan, dan wordt zeker ook voldaan aan (B.6). Dit doen we door de ontwerpeis (B.1) bij de gekozen basisschematisering op te schroeven met een factor γb, de zogenaamde schematiseringfactor. De ontwerpeis wordt dus:

waarin γb> 1 is. Hoe groot γb precies moet zijn om de mogelijke scenario’s Sk+1 … Sn voor de ondergrondopbouw en waterspanningen af te dekken kunnen we al proberend uitzoeken; dit wordt hieronder beschreven.Daarbij moeten we onderscheid maken tussen ‘ontwerpen’ en ‘toetsen’.

Ontwerpen:

Bij het ontwerpen van een dijk of dijkversterking beginnen we met een eerste keuze voor γb. Dit kan een willekeurige waarde zijn tussen 1,0 en 1,3. Op die grenzen komen we later even terug. Stel nu dat de dijk D zo ontworpen wordt dat net voldaan wordt aan (B.8). Dan kunnen ook de stabiliteitsfactoren Fd(D⎪Sk+1) … Fd(D⎪Sn) worden berekend en met behulp van de relatie (B.5) de conditionele faalkansen Pf(D⎪Sk),Pf(D⎪Sk+1) … Pf(D⎪Sn).Hiermee en met de scenariokansen P(Sk+1) …P(Sn) hebben we alle ingrediënten om te controleren of aan de eis (B.7) wordt voldaan.

Wordt niet aan deze eis voldaan, dan is de dijk dus niet voldoende veilig en moet dus een hogere schematiseringfactor worden gekozen, of zou kunnen worden uit- gegaan een conservatiever basisschematisering, bijvoorbeeld Sk+1in plaats van Sk. Dit levert een nieuw ontwerp op, met gewijzigde (hogere) waarden van de stabiliteits- factoren Fd(D⎪Sk+1) … Fd(D⎪Sn), en kan de controle opnieuw worden uitgevoerd.

Wordt heel ruim aan de eis (B.7) voldaan, dan is het natuurlijk ook mogelijk om een lagere schematiseringfactor te kiezen (of een optimistischer basisschematisering, bijvoorbeeld Sk-1 in plaats van Sk). Ook dit geeft een nieuw ontwerp en gewijzigde (lagere) stabiliteitsfactoren, waarmee gecontroleerd moet worden of nog steeds aan de eis (B.7) wordt voldaan.

Merk op dat de schematiseringfactor en de keuze van de basisschematisering ‘uitwisselbaar’ zijn, bij een conservatiever basisschematisering hoort een lagere schematiseringfactor. Moet, volgens de bovenbeschreven controle een schemati-seringfactor groter dan 1,30 worden gekozen, dan is het beter om de basis-schematisering aan te passen (conservatiever te kiezen).

De controlemethode kan eenvoudig als spreadsheettoepassing worden geprogrammeerd. In figuur B.1 is een voorbeeld gegeven. Ter toelichting enkele opmerkingen bij deze figuur:

• Door de gebruiker dient alleen te worden ingevuld (de gele cellen):

• Aan de hand van de formules, die in deze bijlage zijn gegeven, wordt de totale faalkans berekend. Deze wordt vergeleken met de toelaatbare faalkans (zie groene cel met ‘93%’.r
• Tevens wordt in het afgebeelde spreadsheet bijgehouden hoe groot het totaal aan scenariokansen van de ongunstiger scenario’s is (groene cel met ‘0,22’). Aangeraden wordt om de basisschematisering zodanig te kiezen dat de totale kans op een afwijkend ongunstiger scenario niet groter is dan ca. 0,30. Als bij een gekozen basisschematisering de totale kans groter is dan 0,30 dat in werke-lijkheid de opbouw van de ondergrond en waterspanningen ongunstiger is, dan is die basisschematisering niet conservatief te noemen.