repetitie-effect - Bijlage B Probabilistische stabiliteitsanalyse

Repetitie-effect

In deze paragraaf wordt nader ingegaan op de vraag of, bij beschouwing van het repetitie-effect van overleefde historische situaties, de beperking van het uitgangs- punt ten aanzien van ‘random waterspanningsrespons’ tot ‘identieke hoogwater- situaties’ essentieel is of het repetitie-effect ook bij niet identieke hoogwatersituaties kan worden gebruikt. Daarnaast wordt ingegaan op de deterministische pendant (t.b.v. de correctiefactormethode) van de stochastische aanpak voor kwantificering van het repetitie-effect.

Ruwweg gezegd zal bij meer dan één enkele overleefde hoogwatersituatie de kans toenemen dat bij tenminste één daarvan een relatief grote niet systematische stijg- hoogte is gerealiseerd. Dit is de verklaring dat naarmate het aantal overleefde hoogwatersituaties toeneemt het vertrouwen in de sterkte van de dijk toeneemt. In [25] en [28] is een kwantitatieve modellering van dit effect voorgesteld, voor het geval we te maken hebben met identieke overleefde hoogwatersituaties. Voor twee cases is het effect op de bewezen sterkte, in termen van reductie van de faalkans in de toetssituatie, onderzocht. Het resultaat van die exercitie was dat, afhankelijk van de case, de faalkans in de toetssituatie met een factor van 10 respectievelijk 30 af nam bij 10 overleefde hoogwatersituaties in plaats van één. Echter de vraag die zich voordoet is of die modellering ook bruikbaar is wanneer de overleefde historische hoogwatersituaties niet identiek zijn.

Die modellering berust op de volgende redenering. In een overleefde hoogwater- situatie moet gerekend worden met onzekerheid met betrekking tot de in die situatie gerealiseerde niet systematische stijghoogtecomponent. Voor een eenmalige hoog- watersituatie wordt die component gemodelleerd als een stochast met verwach-tingswaarde gelijk nul en een bepaalde standaardafwijking (σw=0,15 m, zie voorgaande paragraaf). Bij twee overleefde hoogwatersituaties is die component twee keer gerealiseerd. We mogen in de ‘Bewezen-Sterkte’-analyse uitgaan van het maximum van de twee realisaties, dat wil zeggen van de verwachtingswaarde en σw en standaardafwijking sσw van het maximum van de rij onafhankelijke realisaties berekenen. In Figuur B 7 zijn m en s gegeven als functie van het aantal repetities. De figuur is gebaseerd op een benadering van de faalkans van een seriesysteem met identieke elementen [3].

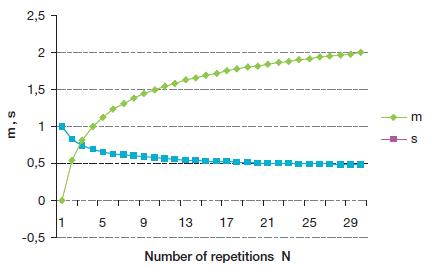
Figuur B 7

m en s als functie van het aantal repetities

Wanneer de overleefde hoogwatersituaties identiek zijn wordt de ‘Bewezen- Sterkte’-analyse uitgevoerd voor de hoogwatersituatie, rekening houdend met verwachtingswaarde en standaardafwijking van de niet systematische waterspan- ningen. Naarmate het aantal overleefde hoogwaters toeneemt, neemt dus ook het waterspanningsniveau in de te analyseren hoogwatersituatie in verwachting toe (en de standaardafwijking iets af), waardoor de a-priori faalkans van de historische hoogwatersituatie toeneemt. Daardoor neemt de a-posteriori faalkans voor de toetssituatie af. Met andere woorden naarmate het aantal overleefde historische hoogwaters toeneemt, neemt ook de bewezen sterkte toe.

Deze aanpak geldt voor identieke overleefde historische hoogwatersituaties. De vraag is hoe de aanpak moet zijn wanneer die hoogwatersituaties niet identiek zijn. Stel we hebben N overleefde historische hoogwatersituaties. Een veilig uit- gangspunt zou zijn om bij de ‘Bewezen-Sterkte’-analyse uit te gaan van de histori- sche hoogwatersituatie met het kleinste belastingeffect. Deze situatie is immers zeker N keer overleefd. Maar we kunnen ook kijken naar de hoogwatersituatie met het op één na kleinste belastingeffect. Deze situatie is immers zeker (N-1) keer overleefd. Of de hoogwatersituatie met het op twee na kleinste belastingeffect, die is (N-2) keer overleefd, enzovoorts, tot de hoogwatersituatie met het grootste belastingeffect, die slecht één keer is overleefd. Voor al die gevallen kunnen we de a-posteriori faalkansen berekenen. Voor de beoordeling van de bewezen sterkte mogen we uitgaan van het geval dat de kleinste a-posteriori faalkans voor de toetssituatie oplevert.

Voor de deterministische analyse (correctiefactoraanpak) kunnen we een soort- gelijk recept opstellen. Uitgangspunt is de opzet van de ‘Bewezen-Sterkte’-analyse, waarbij informatie beschikbaar is over slechts één overleefde historische belasting. Voor de wijze waarop daarbij omgegaan moet worden met niet systematische onzekerheid over waterspanningen wordt verwezen naar de aanwijzingen gegeven in paragraaf B.4. Conform de opzet voor probabilistische analyses bij meerdere overleefde hoogwatersituaties komen we tot de volgende werkwijze bij No overleefde historische belastingen:

1. Beschouw de bewezen sterkte (de opwaartse correctie van de stabiliteitfactor voor de toetssituatie) voor het geval wordt uitgegaan van de historische water- stand met het grootste belastingeffect.

2. Beschouw de bewezen sterkte uitgaande van de historische waterstand met het op één na hoogste belastingeffect. Deze belasting is dus tenminste twee keer overleefd en op basis daarvan mogen we de verwachte waterspanningen voor die belastingsituatie verhogen met de verwachtingswaarde van twee onafhankelijke realisaties van de niet systematische onzekerheid over waterspanningen (dus verhogen met mσw, met m voor N=2 in Figuur B 7)

3. Beschouw de bewezen sterkte uitgaande van de historische waterstand met het op twee na grootste belastingeffect. Deze belasting is tenminste drie keer overleefd en we mogen daarom de verwachte waterspanningen verhogen met mσw, met m voor N=3.

4. Herhaal deze stappen tot en met de historische waterstand met het laagste belastingeffect. Deze belasting is Nokeer overleefd en de verwachte water- spanningen mogen dus opgehoogd worden met mσw, met m voor N=No.

5. De grootste opwaartse correctie van de stabiliteitfactor voor de toetssituatie is maatgevend.