Rekenmodelonzekerheiden - Bijlage B Probabilistische stabiliteitsanalyse

Rekenmodelonzekerheden

Rekenmodellen, voor een stabiliteitsanalyse of voor bijvoorbeeld de berekening van water(over)spanningen, bevatten altijd schematiseringen die soms erg werke- lijkheidsgetrouw zijn en soms ook minder. Er is dus altijd sprake van (onzekere) afwijkingen tussen het resultaat van een berekening en de werkelijkheid. In een probabilistische analyse kan daarmee rekening gehouden door het gebruik van stochastische rekenmodelfactoren. In de probabilistische stabiliteitsanalyses in MPROSTAB en PROLIFT bestaat de mogelijkheid om één rekenmodelfactor te specificeren. Dit is een ‘vuilnisbakfactor’ waarin verschillende mogelijke schema-tiseringonnauwkeurigheden op een hoop gegooid worden. Bijvoorbeeld het feit

dat 3-D effecten bij stabiliteit niet worden meegenomen in het mechanica-model. Maar ook dat, afhankelijk van de manier waarop laboratoriumproeven worden uitgevoerd, de schuifsterkte parameters niet echte bezwijksterkte-parameters zijn. Bijvoorbeeld, de schuifsterkte kan met behulp van triaxiaalproeven worden bepaald. Maar er zijn verschillende proefinterpretatie procedures. Zo kunnen de schuif-sterkteparameters worden bepaald bij 2% of 5% rek van het grondmonster of bij echt bezwijken (pieksterkte). Schuifsterkteparameters die met behulp van een celproef worden bepaald, worden bij zeer lage rekken (1 à 2%) bepaald. Formeel gaat het hierbij niet om rekenmodelonzekerheid, maar onzekerheid (deels systema-tische afwijking) van de totale schematisering en zou dus eigenlijk schematise-ringsonzekerheid moeten heten.

De schematiseringsonzekerheid wordt als volgt in de bovengenoemde reken- modellen voor taludstabiliteit meegenomen. De onderliggende mechanicamodellen hebben als uitkomst een stabiliteitfactor. Die geven we aan met F. Theoretisch, wanneer modelonzekerheid geen rol zou spelen, is er sprake van bezwijken indien F<1 en van evenwicht(sreserve) indien F>1. Indien F=1 zitten we precies op de overgang (de grenstoestand, ook wel ‘limit state’). Praktisch zal ‘1’ niet altijd, of eigenlijk bijna nooit de echte grenstoestand zijn. In genoemde programma’s wordt dit gemodelleerd als:

B8) Z = F - q

Hierin is Z de zogenaamde betrouwbaarheidsfunctie (‘performance function’), Z>0 representeert evenwicht, Z<0 representeert instabiliteit en Z=0 representeert de grenstoestand. De variabele q wordt de drempelwaarde genoemd, die een stochast is met verwachtingswaarde  μq, standaardafwijking σq en waarvan veron- dersteld wordt dat de kansverdeling normaal is. Zou het rekenmodel perfect zijn dan is μq=1 en σq=0. Praktische keuzen, die o.a. zijn gebruikt bij de zogenaamde

‘TAW Marsroute-studies’ [19], zijn weergegeven in Tabel B 1.

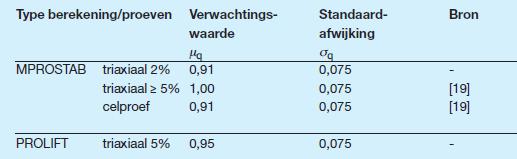
Tabel B 1

Aanbevolen Modelonzekerheidsfactoren