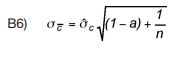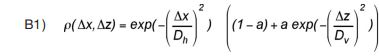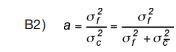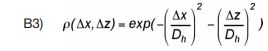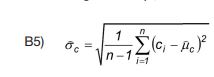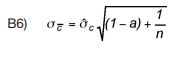Modellering Schuifssterkte - Bijlage B Probabilistische stabiliteitsanalyse

Modellering Schuifsterkte

Het model voor ruimtelijke variatie

De wijze waarop onzekerheid over de schuifsterkte stochastisch wordt gekarakte-riseerd kan verschillen per probabilistisch rekenprogramma. Het basismodel voor beide is een stochastisch model voor de ruimtelijke variatie van de schuifsterkte

binnen een grondlaag (zie ook bijlage 1 ‘Karakteristieke schattingen van de schuif=sterkte’ bij het ‘Technisch Rapport Waterkerende Grondconstructies’ [29], en zie ook hoofdstuk 6, Figuur 12 in de hoofdtekst van dit rapport). In dat model wordt aangenomen dat de schuifsterkte van grond binnen een grondlaag van plaats tot plaats min of meer willekeurig continu kan variëren. Er kan ook sprake zijn van systematische variatie, bijvoorbeeld toename van de schuifsterkte met de diepte. We concentreren ons nu echter even op de willekeurige variaties waarbij we voor het gemak even aannemen dat er geen systematische ruimtelijke variatie is. Het variatiepatroon dat in Figuur 12 getekend is laat de volgende kenmerken zien:

• langs een verticaal varieert de schuifsterkte willekeurig ten opzichte van het gemiddelde over de verticaal (we noemen dit het locale gemiddelde);
• de locale gemiddelden variëren in horizontale richting willekeurig rondom het gemiddelde van het gehele veld (dit noemen we het regionale gemiddelde). Er zijn derhalve relatief sterke en zwakke locale gemiddelden binnen het beschouwde gebied.

Het variatiepatroon wordt gemodelleerd met behulp van een zogenaamde stationair stochastische functie. De parameters van die functie zijn de verwachtingswaarde µc, de standaardafwijking σc en zogenaamde autocorrelatieparameters (behorende bij een autocorrelatiefunctietype). Een autocorrelatiefunctie die het in Figuur 12 geschetste variatiepatroon goed karakteriseert is:

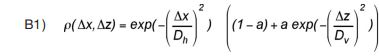
Hierin is ρ(Δx, Δz) de correlatie tussen de schuifsterktes in twee punten binnen de grondlaag met een onderlinge afstand van Δx in horizontale en Δz in verticale richting. De parameters Dh en Dv zijn autocorrelatieparameters, respectievelijk voor uitdemping van correlatie in horizontale en in verticale richting. De parameter a representeert de verhouding van de locale en de totale regionale variantie:

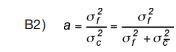
Indien a=1 is de variantie van de spreiding σf 2 ten opzichte van het locale gemid-delde net zo groot als de spreiding ten opzichte van het regionale gemiddelde, en derhalve de spreiding van de locale gemiddelden σc _ 2 ten opzichte van het regionale gemiddelde gelijk nul. De autocorrelatiefunctie is dan gelijk aan:

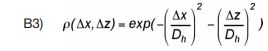
Dit type autocorrelatiefunctie wordt in de literatuur vaak aanbevolen. Echter daarmee kunnen geen velden met relatief sterke en zwakke locale gemiddelden worden gemodelleerd. Bij het opzetten van proevenverzamelingen in een klein gebied (met afmetingen in horizontale richting van zeg tientallen tot honderd à tweehonderd meter) is dat een plausibele aanname. Bij het opzetten van proevenverzamelingen (regionale proevenverzamelingen) in een groot gebied (zeg enkele tot vele kilo-meters) zijn juist aanwijzingen gevonden voor de aanwezigheid van relatief sterke en zwakke locaties. Daarom is als modelleringuitgangspunt gekozen voor een autop-correlatiefunctie van het type volgens vergelijking (B 1). In onder andere bijlage 1 bij het Technisch Rapport Waterkerende Grondconstructies is aangegeven dat dit consequenties heeft voor de wijze waarop karakteristieke schattingen van de schuif-sterkte van de grond aan de hand van de proevenverzameling worden bepaald

Schuifsterkte in het rekenmodel voor stabiliteitsanalyse

Gevolg van de ruimtelijke variatie is dat de schuifsterkte van punt tot punt langs een glijcilinder (of ander glijvlak) varieert. In de terminologie van de lamellenmethode van Bishop: op elke lamelonderkant werkt (zelfs binnen één en dezelfde grondlaag) een andere schuifsterkte. In de praktijk is het natuurlijk ondoenlijk om voor elke lamelonderkant de precieze schuifsterkte te bepalen. Gelukkig is dat ook niet nodig, omdat in de berekening die schuifsterktes gesommeerd worden. Eigenlijk is dus de gemiddelde schuifsterkte langs het glijvlak (binnen de betreffende grond-laag) van belang. In de praktijk wordt dan ook gerekend met gemiddelde schuif-sterktes in de grondlagen die door het glijvlak doorsneden worden. Dat moeten uiteraard de gemiddelden zijn op de locatie van het glijvlak dat onderzocht wordt, zogenaamde locale gemiddelden.

Gevolg van de modellering van het variatiepatroon als stochastische functie is dat de gemiddelde schuifsterkte binnen een grondlaag (in feite langs het deel van het glijvlak binnen de grondlaag) een stochastische variabele is. De verwachtings-waarde van dat gemiddelde komt overeen met de verwachtingswaarde van het ruimtelijke variatiemodel, µc. De standaardafwijking van dat gemiddelde is kleiner dan de standaardafwijking σc van het ruimtelijke model. Immers, door integratie langs het glijvlak wordt de ‘punt’ variatie deels uitgemiddeld. Het al dan niet mee-nemen van het uitmiddelingproces in de probabilistische stabiliteitsanalyse is er de oorzaak van dat voor verschillende rekenmodellen de invoer voor schuifsterk-teparameters verschillend is. Bijvoorbeeld:

• In het programma MPROSTAB wordt het uitmiddelingproces expliciet mee-genomen in de berekening. Dat houdt in dat in elke lamelonderkant van het glijvlak de schuifsterkteparameter een trekking is uit het ruimtelijke stochasti-sche model. Schuifsterktes in opvolgende lamelonderkanten zijn in principe verschillend, hoewel wel gecorreleerd volgens de correlatiefunctie (B 1). Het uitmiddelingproces wordt meegenomen in de sommatie van lamelbijdragen aan het totale tegenwerkende moment. In dit programma moeten dan ook de ‘punt’standaardafwijking van het ruimtelijke model σc , de correlatieparameters Dh en Dv en de variantieverhouding a worden opgegeven.
• In de PROLIFT module van MSTAB wordt per grondlaag de verwachtings-waarde en de standaardafwijking van de gemiddelde schuifsterkte binnen de grondlaag verwacht als invoer. Hier behoeven dus geen autocorrelatiepara-meters te worden opgegeven. De verwachtingswaarde is gelijk aan de ver-wachtingswaarde van het ruimtelijke model, µc. De standaardafwijking van de gemiddelde schuifsterkte langs het (deel van het glijvlak) dat de grondlaag doorsnijdt moet eigenlijk via een ingewikkelde uitmiddelingberekening worden bepaald. Een redelijke benadering is echter 

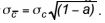
In de rekenvoorbeelden is aangegeven hoe in beide gevallen de invoerparameters dienen te worden bepaald. De autocorrelatieparameters zijn geen ‘bekende’ grootheden binnen de adviespraktijk en zijn ook niet zonder uitgebreid onderzoek vast te stellen. In het rekenvoorbeeld met MPROSTAB wordt aangegeven dat met ‘standaardwaarden’ kan worden gerekend. Daarbij wordt er van uitgegaan dat in verticale zin snelle uitmiddeling plaats zal vinden; standaard kan met een verticale autocorrelatieparameter Dv=0,25 m en een horizontale correlatieparameter Dh= 50 m worden gerekend. Voor de variantieverhouding a is de keuze afhankelijk van het type proevenverzameling op basis waarvan verwachtingswaarde en standaardafwijking worden geschat (zie ook bijlage 1 bij het ‘Technisch Rapport Waterkerende Grondconstructies’ [29]). Gaat het om een regionale proeven-verzameling, dan kunnen we de waarde van a kiezen conform het recept voor het bepalen van de karakteristieke schuifsterkte in de ‘Leidraad voor het ontwerpen van rivierdijken, deel 2 – benedenrivierengebied’ [4]: (1-a)=Γ 2 met Γ=0,5. Gaat het

om een proevenverzameling op basis van locaal grondonderzoek dan is a=1 een voor de hand liggende keuze.

Statistische onzekerheid

Naast ruimtelijke variatie hebben we te maken met statistische onzekerheid. De verwachtingswaarde µc. en de standaardafwijking σc van het ruimtelijke model zijn geen gegeven grootheden, maar moeten worden geschat aan de hand van (laboratorium)proeven op grondmonsters. Aan de hand van een proevenserie worden schattingen van de verwachtingswaarde en de standaardafwijking berekend. Veronderstel dat een serie proeven op grondmonsters wordt uitgevoerd. De uitkomst van elke proef is de schuifsterkte van het betreffende grondmonster. We nemen even aan dat de schuifsterkte gekarakteriseerd kan worden door één getal, bijvoorbeeld c, de ongedraineerde cohesie. De uitkomst van de proevenserie geven we aan met {c1, c2, c3, …cn}. De verwachtingswaarde van c wordt als volgt geschat:

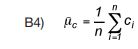
waarin 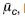 het rekenkundig steekproefgemiddelde, een zuivere schatter is voor de verwachtingswaarde µc. De standaardafwijking van c wordt geschat met:

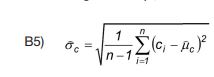
Hierin is σc de standaardafwijking van de steekproef. Deze is een zuivere schatter van de standaardafwijking σc van het ruimtelijke model. Als de puntwaarden van c binnen de grondlaag een normale verdeling hebben met verwachtingswaarde µc en standaardafwijking σc, dan is de schatter ook normaal verdeeld, met ver-wachtingswaarde µc en standaardafwijking σc /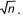 

Met andere woorden, wanneer we in een probabilistische stabiliteitsanalyse het steekproefgemiddelde gebruiken om de verwachtingswaarde van de schuifsterkte te karakteriseren, moeten we rekening houden met de mogelijke afwijking tussen dit gemiddelde en de werkelijke verwachtingswaarde (dit heet de statistische onzekerheid). In de genoemde programma’s wordt dat verschillend opgelost:

• In het programma MPROSTAB gebeurt dit door het programma zelf. Naast schattingen van de verwachtingswaarden en standaardafwijkingen ( 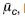en σc ) van de schuifsterkteparameters in de verschillende grondlagen moet ook het aantal proeven waarop de schatting van de verwachtingswaarde is gebaseerd worden opgegeven. In het rekenprogramma wordt dan uitgegaan van een statistische onzekerheid van opgegeven verwachtingswaarde waarvan de standaardafwijking gelijk is aan .  σc/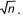 
• In de PROLIFT-module binnen MSTAB is niet zo’n rekenmechanisme aanwezig. Bij dit programma wordt ervan uitgegaan dat statistische onzekerheid in de opgegeven schatting van de verwachtingswaarde verdisconteerd is in de opge-geven schatting van de standaardafwijking van de schuifsterkte per grondlaag. De standaardafwijkingen voor ruimtelijke variatie van locale gemiddelden en de statistische onzekerheid moeten derhalve gecombineerd worden. De op te geven standaardafwijking is: