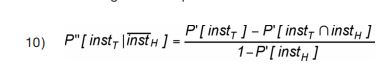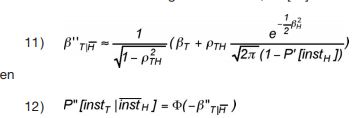Invloed van één overleefde belastingsituatie - Methode ‘Probabilistische Stabiliteitsanalyse’

Invloed van overleefde belasting (bewezen sterkte)

Invloed van één overleefde belastingsituatie

Onder een overleefde belastingsituatie wordt doorgaans verstaan een hoogwater-situatie in het verleden die zonder problemen ten aanzien van de stabiliteit is door-staan. Voor zover de wijze waarop een hoge waterstand de sterkte van de water-kerende constructie aanspreekt en ook die sterkte zelf sinds de historische belastingsituatie niet in ongunstige zin is veranderd, levert het overleven nuttige informatie voor de veiligheidstoetsing. In hoofdstuk 4 is nader ingegaan op voor-waarden ten aanzien van de betrouwbaarheid van historische informatie en op richtlijnen hoe deze informatie te gebruiken bij deterministische veiligheidstoets-ingen. In deze paragraaf wordt nader ingegaan op de probabilistische aanpak bij het meenemen van een overleefde historische belasting. Voor onderbouwing van dit concept wordt ook verwezen naar [27] en [45].

Het begrip ‘Bayesian updating’ van instabiliteitkansen speelt een centrale rol. Daarbij worden eerst de historische en de toetssituatie (belastingssituatie voor de veiligheidstoetsing) afzonderlijk beschouwd. Voor beide situaties kunnen instabili-teitkansen worden berekend, zoals beschreven in de voorgaande paragrafen. Die kansen worden aangeduid als de a-priori instabiliteitkansen. Ze zijn gebaseerd op informatie betreffende waterstanden, geschatte verwachtingen en spreidingen van de hieruit voortvloeiende waterspanningen en geschatte verwachtingen en spreidingen van de grondeigenschappen. Kortom de informatie die vooraf beschikbaar is als we een schatting van de kans op instabiliteit voor de toets-situatie bepalen. Het gegeven dat in de historische situatie geen instabiliteit is opgetreden (ondanks dat er wel een kans was dat dit zou gebeuren) is nieuwe informatie welke wordt gebruikt om de kans op instabiliteit in de toetssituatie bij te stellen. Die bijgestelde kans wordt de a-posteriori instabiliteitkans genoemd. De basisuitdrukking voor de a-posteriori instabiliteitkans is:

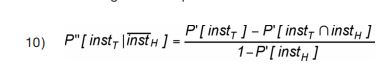
waarin:

P’[instΤ ] = A-priori instabiliteitkansen in de toetssituatie P’[instΗ ] = A-priori instabiliteitkansen in de historische hoogwatersituatie

= de kans op instabiliteit die berekend zou worden zonder gebruik te maken van het gegeven dat die belastingsituatie feitelijk is overleefd

P” [instΤ \ instΗ ] = A-posteriori instabiliteitkans in de toetssituatie, gegeven het overleven van (het níet optreden van instabiliteit in) de historische belastingsituatie.

P’[instΤ ∩ instΗ ]. = Kans op het optreden van instabiliteit in zowel de historische als de toetssituatie, zoals die berekend zou worden als niet bekend zou zijn dat de historische belastingsituatie feitelijk overleefd is. Deze kans is sterk afhankelijk van de correlatie tussen de bezwijkmechanismen in de historische en de toetssituatie.

Die correlatie is het gevolg van aannamen over hoe onzekerheden over belasting-effecten en sterkte in beide belastingsituaties worden gerealiseerd. Voor de grond-eigenschappen wordt aangenomen dat de precieze grootte van, bijvoorbeeld, de schuifsterkte op zich weliswaar niet bekend is, maar dat die wel gelijk is in beide belastingsituaties. Hetzelfde geldt min of meer ook voor de rekenmodel-onzeker-heid. Het rekenmodel heeft een bepaalde onnauwkeurigheid. We weten niet hoe groot de afwijking tussen model en werkelijkheid als gevolg van beperkingen van het rekenmodel is. Maar, als de bezwijkmechanismen in beide situaties erg op elkaar lijken mag aangenomen worden dat die afwijkingen voor beide belastings-ituaties ongeveer gelijk zullen zijn. Bij de waterspanningen, daarentegen, zullen onzekerheden in historische en toetssituatie zich althans deels verschillend kunnen realiseren. Immers, de feitelijk gerealiseerde waterspanning in een belastingsitua-tie is, naast de hoogwaterstand en hoogwaterstandduur, ook afhankelijk van de neerslaggeschiedenis voorafgaande aan de belastingsituatie. Een deel van de waterspanningsonzekerheid, met name van freatische waterspanningen, reflecteert neerslageffecten. De neerslageffecten voorafgaande aan de historische hoog-waterbelasting en een eventuele met de toetssituatie overeenkomende toekomstige hoogwaterstand zijn met grote kans verschillend. De realisaties van het deel van de waterspanningsonzekerheden in historische en toetssituatie, die het gevolg zijn van neerslageffecten, moeten dus als ongecorreleerd worden beschouwd.

De correlatie tussen de bezwijkmechanismen in historische en toetssituatie kan aan de hand van de uitkomsten van de a-priori stabiliteitsanalyses worden geschat. Deze analyses hebben, zoals gezegd, naast de schatting van de instabiliteitkans ook probabilistische invloedscoëfficiënten als uitkomst. Met behulp van die coëffi-ciënten kan de correlatiecoëfficiënt tussen de bezwijkmechanismen in historische en toetssituatie berekend worden. Bij de bespreking van de modelleringaspecten (Bijlage B) zullen we daar nader op ingaan. De correlatiecoëfficiënt geven we aan met ρTH.

De a-posteriori instabiliteitkans voor de toetssituatie, dus gebruikmakend van het gegeven dat de historische belastingsituatie is overleefd, kan nu met gegeven ρTH worden berekend met de volgende formules, zie [45]:

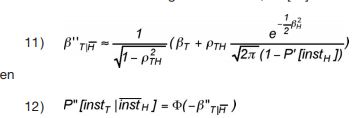
waarin:

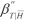 = de (a-posteriori) betrouwbaarheidsindex voor de toetssituatie, gegeven het overleven van de historische belastingsituatie

βH = de betrouwbaarheidsindex voor de historische belastingsituatie (beho-rend bij de a-priori instabiliteitkans)

βT = de betrouwbaarheidsindex voor de toetssituatie (behorend bij de a-priori instabiliteitkans)

Aan de hand van vergelijking (11) zien we dat indien de correlatiecoëfficiënt zeer klein is, dat dan de a-posteriori betrouwbaarheidsindex ongeveer gelijk is aan de a-priori betrouwbaarheidsindex voor de toetssituatie, ofwel ≈ βT. Daarmee is dus ook de a-posteriori kans op instabiliteit in de toetssituatie ongeveer gelijk aan de a-priori instabiliteitkans. Het gegeven dat de historische belastings-situatie is overleefd voegt derhalve in geval van geringe correlatie tussen historische situatie en toetssituatie geen informatie over de sterkte in de toetssituatie toe.

Is de correlatiecoëfficiënt groot, bijvoorbeeld bijna 1, dan is het effect op de instabiliteitkans in de toetssituatie groot, ofwel ≈ βT.

In dat geval is overleven van de historische belastingsituatie een zeer relevant gegeven voor de toetssituatie.

Een globale indicatie voor correlatiecoëfficiënten is de range 0,6 - 0,95. In Tabel 8 is het aan de hand van vergelijking (10) berekende effect van variatie van de correlatiecoëfficiënt weergegeven voor de volgende gegevens:

• βH = 0,5 overeenkomend met een instabiliteitkans P’[instH] = 0,31;
• βT = 0,4 - 1,6 overeenkomend met instabiliteitkansen P’[instT] = 0,34 - 0,05;
• range van correlaties ρTH = 0,65 - 0,95.

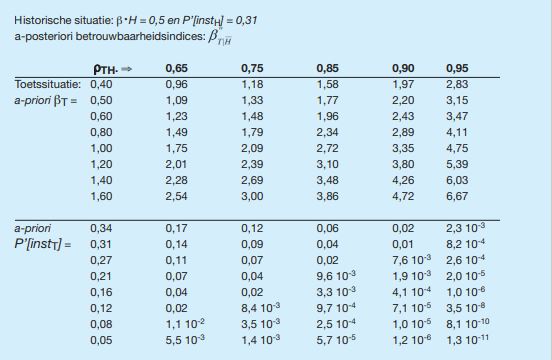
Tabel 8

Sondeerafstanden waarbij de kans op voorkomen van een pakketdikte kleiner dan 8m minder dan 5% is als functie van de gevonden minimale pakketdikte bij sonderen

De berekeningresultaten in de tabel laten zien dat:

• de a-posteriori betrouwbaarheidsindex groter is naarmate de a-piori betrouw-baarheidsindex voor de toetssituatie groter is dan voor de historische belasting-situatie. Of in termen van faalkansen: dat de a-posteriori faalkans kleiner is naarmate de a-priori faalkans voor de toetssituatie kleiner is dan die voor de historische belastingsituatie.
• dit effect sterker is naarmate de correlatie tussen de maatgevende mechanismen (glijcirkels of andere glijvlakken) in de toetssituatie en de historische belasting-situatie groter is.

Het beoogde resultaat is doorgaans een kleine a-posteriori faalkans, in de orde van, zeg, 10-4 à 10-6. Dit betekent dat de a-priori faalkans in de historische situatie eigenlijk niet kleiner mag zijn dan in de toetssituatie én dat de correlatie tussen de maatgevende mechanismen in historische en toetssituatie groot moet zijn. Het eerste houdt praktisch in dat de belasting in de overleefde historische situatie niet kleiner mag zijn dan in de toetssituatie. Het laatste dat de “aangesproken” (grond)sterkte in de beide situaties ongeveer dezelfde moet zijn (dus dat de maat-gevende glijvlakken niet erg ver uit elkaar liggen) en dat het ‘niet systematische’ deel in de onzekerheid over de waterspanningen, niet mag overheersen.

Dat laatste behoeft enige toelichting. Het effect van de waterstand is de ontwik-keling van waterspanningen in de dijk en de ondergrond. Die waterspanningen beïnvloeden de effectieve grondspanningen en daarmee het deel van de schuif-sterkte dat geleverd wordt door de inwendige wrijving. Onzekerheden over de aanwezige, met name freatische, waterspanningen worden niet alleen veroorzaakt door onzekerheid over de waterspanningsrespons in de dijk op de buitenwater-stand, maar ook door waterspanningen die bij het begin van hoge buitenwater-stand al aanwezig waren als gevolg van de neerslaggeschiedenis gedurende enige tijd voorafgaande aan de hoge waterstand. De onzekerheid van de (freatische) waterspanningen bestaat dus uit twee delen, namelijk een deel dat voortkomt uit de berekening van de waterspanningsrespons op de buitenwaterstand, dus een soort berekeningsonzekerheid, en een deel dat gerelateerd is aan de neerslag-geschiedenis. Van de eerste kunnen we veronderstellen dat deze in de historische en de toetssituatie onderling afhankelijk zullen zijn; omdat in de historische situatie en de toetsituatie de responskarakteristieken niet veel af zullen wijken, althans wanneer de geohydrologische configuratie van de dijk en de ondergrond niet is gewijzigd. Was de waterspanningsopbouw in de historische situatie hoger dan volgens de berekeningen verwacht zou worden, dan zal dat ook in de toetssituatie zo zijn en vice versa. Dit deel van de waterspanningsonzekerheid noemen we daarom ‘systematisch’. Van de aan neerslag gerelateerde waterspanningsonzeker-heden kunnen we dat niet zonder meer veronderstellen. Stel immers, dat het aan-deel in de onzekerheid van de waterspanningen als gevolg van neerslag groot is ten opzichte van het aandeel dat het gevolg is van de berekeningsonzekerheid van de respons op de buitenwaterstand. Als we geen informatie hebben over de neerslag voorafgaande aan de historische waterstand, dan kunnen we achteraf niet duiden of die is overleefd omdat de grond sterker is dan gedacht, of omdat de historische hoogwatersituatie toevallig samenviel met een zeer droge periode. Voor de toetssituatie moeten we uiteraard wel rekening houden met een bijdrage aan de (onzekerheid over) waterspanningen als gevolg van neerslag. In dit geval is dus de onzekerheid over waterspanningen die gerelateerd is aan neerslag ‘niet systematisch’ voor historische en toetssituatie.

In de ‘Bewezen-Sterkte’-analyse, zie Bijlage B, is dit van belang voor de keuze van de correlatie tussen waterspanningsonzekerheden in historische en toetssituatie. De correlatie in vergelijking (11) en in Tabel 8 is afhankelijk van de gekozen corre-laties tussen waterspanningsonzekerheden in historische- en toetssituatie en de correlatie tussen schuifsterkte(parameters) in historische- en toetssituatie. De laatste kunnen doorgaans op 1.0 worden gesteld, omdat de kern van het ‘Bewezen-Sterkte’-concept is dat dezelfde grond wordt aangesproken en dat dus de schuifsterkteparameters voor de historische en de toetssituatie, hoewel op zich niet exact bekend hoe groot, wel gelijk zijn.

De hier gegeven beschouwing is richtinggevend voor de beoordeling van de bruikbaarheid en effectiviteit van het ‘Bewezen-Sterkte’-concept voor een bepaal-de toetssituatie op basis van een overleefde hoogwatersituatie en geldt zowel voor de hier geschetste probabilistische aanpak, als voor de in hoofdstuk 4 geschetste deterministische aanpak.