Deze koppeling van de fragmenten levert twee lineaire algebraïsche vergelijkingen waarmee de onbekende Φ 1,2en Φ 2,3kunnen worden opgelost.
Het laat zich raden dat de methodiek rechttoe rechtaan uit te breiden is tot een willekeurig aantal achter elkaar geschakelde fragmenten. De kracht van de methode is dat voor een aantal standaardtypen van fragmenten de weerstandsfactoren met behulp van complexe functietheorie kunnen worden berekend. Met deze standaardtypen kunnen betrekkelijk ingewikkelde stromingsconfiguraties onder een dijk of kunstwerk worden samengesteld. Het koppelen van de fragmenten kan met behulp van eenvoudige berekeningen worden uitgevoerd.
Voor het mechanisme heave is het optredende verticale verhang over het kwelscherm in het staartfragment van belang. In Figuur A.2 is dit:
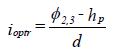 A(1.20)
A(1.20)
Dit verhang moet kleiner zijn dan het toelaatbare verhang itoel = 0,5.
Voor het uitvoeren van berekeningen met de fragmentenmethode is een spreadsheetprogramma ontwikkeld. In de spreadsheetberekeningen kan het optredende verticale verhang gemakkelijk gekoppeld worden aan het totale verval (H-hp) over de waterkering. Met behulp hiervan kunnen zogenaamde afleesgrafieken worden opgesteld
waarin het toelaatbare verval over de kering kan worden afgelezen als functie van ontwerpparameters, zoals bijvoorbeeld de lengte van de kwelschermen in relatie tot de dikte van de zandlaag. In Figuur A.4 is’zo'n afleesgrafiek weergegeven. Op de horizontale as staat de relatieve inbedding d/D uitgezet en op de verticale as de verval ratio itoel*L/(H-hp). De grafiek hoort bij een configuratie met twee even lange kwelschermen. Bij een gegeven totale verval (H-hp) over de kering, de lengte L van de kering en het aan te houden criterium voor heave, itoel, is de benodigde relatieve schermlengte (althans de relatieve inbedding in de zandlaag) d/D af te lezen. Met sterren is in deze grafiek aangegeven hoe de grafiek er uit zou zien, wanneer in plaats van met de fragmentenmethode gewerkt zou worden met het numerieke grondwaterstromingsprogramma MSEEP. We zien dat voor waarden van de inbeddingslengte d groter dan 0,2D de fragmentenberekening en de MSEEP berekening zeer nauw aansluiten. Voor inbeddingslengten kleiner dan 0,1D zijn de berekeningen met de fragmentenmethode onnauwkeurig. Aanbevolen wordt om de minimaal benodigde inbeddingslengte gelijk aan 0,1D te kiezen.
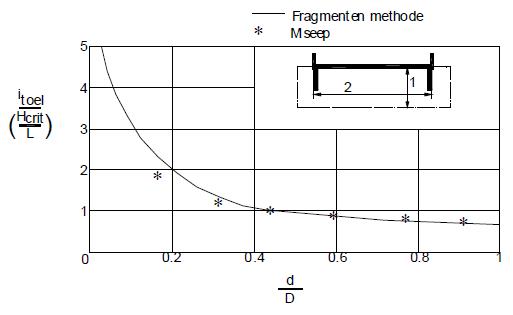
Figuur A.4 Afleesgrafiek toelaatbaar verval over waterkering i.v.m. Heave
In de fragmentenanalyses wordt in beginsel uitgegaan van isotrope doorlatendheid van de zandlaag. De horizontale en verticale doorlatendheden kunnen echter verschillend zijn, bijvoorbeeld door aanwezigheid van horizontale stoorlaagjes of lensjes. In de meeste gevallen kan dit verdisconteerd worden door de fragmenten (verticaal of horizontaal) te verschalen. Aanbevolen wordt echter om hierbij een deskundige te raadplegen.
De afleesgrafiek geldt voor een situatie waarin er een goede aansluiting is tussen de onderkant van de kering en de bovenkant van de zandlaag. Indien die aansluiting er niet is, of wanneer dit onzeker is, moet de weerstandsfactor voor het middenfragment worden gereduceerd; zie ook [Calle & Sellmeijer, 1998].
De bovengenoemde fragmenten kunnen worden gebruikt voor het modelleren van het heave- probleem bij kunstwerken of dijken zonder deklaag in voor en achterland. Die fragmenten zijn:
-
het kopfragment (Figuur A.3a)
-
het tussenfragment (Figuur A.3b)
-
het staartfragment (Figuur A.3c)
In beginsel zijn configuraties te modelleren door schakeling van één kopfragment, een of meer tussenfragmenten en één staartfragment. De oplossingsmethodiek is geïmplementeerd in het spreadsheet-programma HEAVE (zie Bijlage C); hierin zijn maximaal 6 tussenfragmenten te specificeren.
Voor twee eenvoudige basisconfiguraties zijn met behulp van dit programma grafieken afgeleid voor toetsing op heave bij kunstwerken of dijken met één of twee kwelschermen (zie Figuur A.5). Bij de berekening van het toelaatbare verhang over de kering is uitgegaan van isotrope doorlatendheid van de zandlaag en een toelaatbaar verticaal verhang aan de benedenstroomse zijde van de kering van 0.5. De grafiek voor één enkel kwelscherm aan de benedenstroomse zijde van de kering (Figuur A.5b) is ontleend aan de Leidraad Toetsen op Veiligheid [TAW, 1996]. De wijze van gebruik van de grafieken ligt voor de hand. Verderop in deze bijlage zijn tabellen voor weerstanden van fragmenten gegeven, waarmee de gebruiker zelf een fragmentenanalyse kan uitvoeren. Hiermee is het mogelijk om de basisconfiguratie voor de grafieken, maar dan met verschillende lengten van de damwanden aan boven- en benedenstroomse zijde, door te rekenen. Ingeval de actuele configuratie zodanig afwijkt dat de grafieken of de tabellen niet te gebruiken zijn kan de toetsing met behulp van het spreadsheetprogramma zelf worden uitgevoerd.
In het kader van onderzoek voor de TAW [Calle & Sellmeijer, 1998] zijn nog verschillende andere fragmenttypen ontwikkeld, namelijk:
-
het ‘zettingsfragment’, waarmee het effect van vrije ruimte tussen de onderkant van een kunstwerk en de zandlaag (een ‘zettingsspleet’) op het mechanisme heave kan worden onderzocht;
-
‘lekfragmenten’, waarmee de invloed van lek door de sloten van de kwelschermen, of geconcentreerde lek door een (corrosie-)gat kan worden onderzocht; dit is van belang voor het toetsen van waterkeringen, waarbij men onzeker is van de conditie van de kwelschermen;
-
het ‘voorlandfragment’, waarmee de invloed van een afdekkende laag in het voorland kan worden onderzocht;
Deze fragmenten zijn en worden vooralsnog alleen gebruikt in het kader van onderzoek, o.a.:
-
een probabilistische gevoeligheidsstudie van de invloed van zettingsspleten en lek door de kwelschermen op het mechanisme heave [Calle & Sellmeijer, 1998];
-
integratie van piping- en heave-regels [Sellmeijer, 1996].
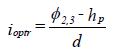 A(1.20)
A(1.20)