De Fragmentenmethode
Het principe van de Fragmentenmethode
In opdracht van de TAW (thans ENW) is een rekentechniek ontwikkeld, speciaal voor het analyseren van de grondwaterstroming onder dijken of kunstwerken met kwelschermen. Het is een semi-analytische techniek, die als voordeel boven een numerieke grondwaterstromingsanalyse heeft dat zeer snel berekeningen kunnen worden uitgevoerd. Het principe wordt hieronder beschreven, voor details wordt verwezen naar o.a. (Van de Paverd, 1994), (Sellmeijer, 1995) en (Sellmeijer, 1997). Het basisidee voor de methodiek is van minder recente datum (Pavlovsky, 1956).
Beschouw de configuratie van een waterkering, in dit geval een kunstwerk, met een tweetal kwelschermen, in Figuur A.2. In de figuur zijn de randvoorwaarden voor grondwaterstroming door de zandlaag onder de constructie aangegeven, namelijk de stijghoogte gelijk aan de buitenwaterstand aan het oppervlak van de zandlaag bovenstrooms en de stijghoogte gelijk aan de binnenwaterstand benedenstrooms. De totale configuratie met kwelschermen is te ingewikkeld voor een directe analytische oplossing van het grondwaterstromingsprobleem. Daarom wordt het geheel opgedeeld in, in dit geval, drie stukken, namelijk een kopfragment (fragment 1), een tussenfragment (fragment 2) en een staartfragment (fragment 3). De scheidingen tussen de fragmenten zijn verticale lijnen in het verlengde van de kwelschermen. De crux van de methode is dat deze lijnen bij benadering equipotentiaallijnen zijn (lijnen met constante stijghoogte). De potentiaal op de scheidslijn tussen fragment 1 en fragment 2 is dus te karakteriseren door één waarde, Φ 1,2, die echter vooralsnog onbekend is. Zo ook de potentiaal op de scheidslijn tussen fragment 2 en fragment 3, namelijk Φ 2,3.
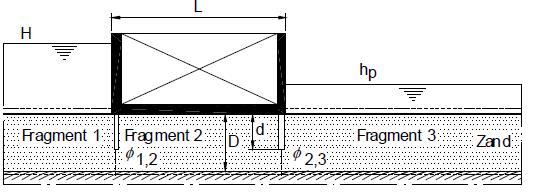
Figuur A.2 Opdelen in fragmenten
Vervolgens kunnen de fragmenten afzonderlijk worden beschouwd. In Figuur A.3(a) is het kopfragment geschetst en zijn de randvoorwaarden voor de stroming binnen dit fragment aangegeven. Het grondwaterstromingsprobleem kan met behulp van technieken uit de complexe functietheorie worden opgelost, wanneer een bepaalde waarde voor de potentiaal Φ 1,2 wordt aangenomen. Met de gegeven doorlatendheid van de grond binnen dit fragment kan derhalve het debiet dat door dit fragment stroomt, dat wil zeggen langs de bovenrand binnenkomt en langs scheidingslijn het fragment weer verlaat, worden bepaald. Dit debiet geven we aan met Q. We weten dat dit debiet recht evenredig moet zijn met de doorlatendheid k1 en met het (aangenomen) verval (H - Φ 1,2) over het fragment. Met behulp van de berekende Q wordt het quotiënt:
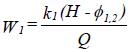 A(1.18)
A(1.18)
bepaald. Dit quotiënt is, vanwege genoemde evenredigheid, onafhankelijk van de keuze van k1en Φ 1,2en wordt de weerstandsfactor van fragment 1 genoemd.
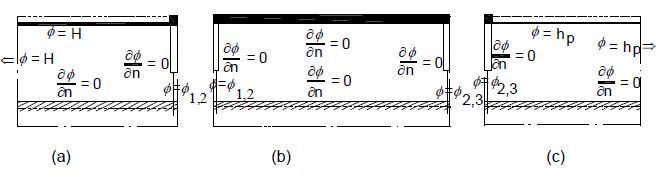
Figuur A.3 (a) kopfragment, (b) tussenfragment en (c) staartfragment
Op analoge wijze kunnen ook de weerstandsfactoren W2en W3in de fragmenten 2 en 3 (Figuur A.3 b en c) worden bepaald. Om de potentiaalverdeling te berekenen maken we gebruik van het feit dat de doorstroomdebieten door elk van de fragmenten gelijk moeten zijn aan elkaar, dus:
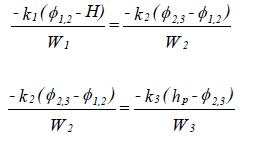 A(1.19)
A(1.19)

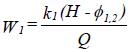 A(1.18)
A(1.18)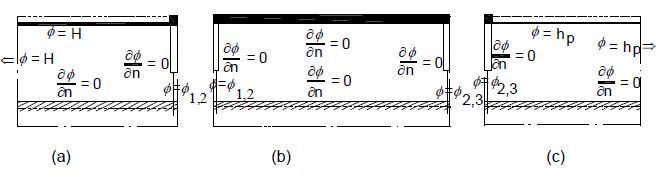
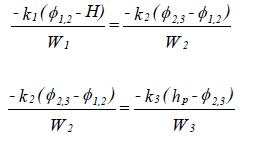 A(1.19)
A(1.19)