In geval tijdsafhankelijkheid een rol speelt, bij kort durende of cyclische buitenwaterstanden, speelt bij de verticale stroming door de deklagen in voor- en achterland consolidatie (voorland) en zwel (achterland) een rol. Omdat hierdoor de gradiënten van de stijghoogten onderin de deklagen, (in absolute waarde) groter zijn dan in de stationaire situatie hebben we te maken met (tijdelijk) grotere instroomdebieten in de zandlaag ter plaatse van het voorland en grotere uitstroomdebieten vanuit de zandlaag naar de deklaag in het achterland. Dit leidt tot kleinere spreidingslengten en daardoor tot een kleiner gebied, waarin de stijghoogte in de zandlaag vervalt van buitenwaterstand (H) tot polderpeil (hp).
De beschrijvende vergelijkingen zijn een gekoppeld stelsel van consolidatie vergelijkingen in de deklagen en de Dupuit-stromingsvergelijking in de zandlaag. De vergelijking voor verticale stroming door de deklaag in de gebieden I en III (zie Figuur A.1) luidt:
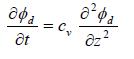 A(1.10)
A(1.10)
Hierin is Φd (z,t;x) de stijghoogte in de deklaag, dit is voor elke x een functie van z en t, met als randvoorwaarde op z = 0, de grens met de watervoerende zandlaag, de stijghoogte Φz (x) in de zandlaag en als randvoorwaarde op z = d de (momentane) buitenwaterstand in gebied I en het maaiveld- of polderpeil in gebied III. In gebied I is cv de consolidatiecoëfficiënt en in gebied III de zwelcoëfficiënt; in gebied II wordt, analoog aan het stationaire berekeningsmodel geen lek vanuit de zandlaag naar de dijkskern of omgekeerd verondersteld. De horizontale stroming door de watervoerende zandlaag wordt beschreven door de vergelijking:
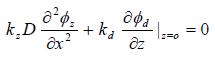 A(1.11)
A(1.11)
Hierin is Φz(x) de stijghoogte in de zandlaag. In gebied II vervalt de term in het linkerlid van vergelijking A(1.11). De aansluitingsvoorwaarde (continuïteit van stijghoogte in zand- en deklaag) in de gebieden I en III luidt:
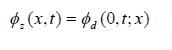 A(1.12)
A(1.12)
In het programma WATEX worden deze vergelijkingen opgelost. We kunnen twee karakteristieke situaties onderscheiden, namelijk:
- De buitenwaterstand is een niet periodieke tijdsafhankelijke functie. In WATEX kan daarvoor een blokfunctie worden opgegeven:
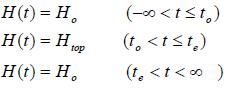 A(1.13)
A(1.13)
In dat geval is de beginvoorwaarde voor het probleem de stationaire situatie die hoort bij de waterstand Ho. De vergelijkingen A(1.11) … A(1.13) worden opgelost met behulp van Laplace-transformaties.
- De buitenwaterstand is een periodieke functie:
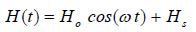 A(1.14)
A(1.14)
In dit geval bestaat de (steady state) oplossing uit superpositie van de stationaire oplossing bij de randvoorwaarden Φ (-Lv) = Hsen Φ (∞) = hp, en een cyclische component. De cyclische component wordt berekend met behulp van een complexe harmonische analyse.
Voor het geval de buitenwaterstand een periodieke functie beschouwen we de oplossing. Eenvoudigheidshalve nemen we aan dat voor- en achterland oneindig breed zijn, dat de breedte van het gebied II verwaarloosbaar klein is en dat de stationaire component van de buitenwaterstand Hsgelijk is aan het polderpeil hp. De oplossing voor de stijghoogte in de zandlaag in gebied I luidt, wanneer de hydrodynamische perioden van de deklagen groot zijn ten opzichte van de periode (2 π / ω) waarmee de buitenwaterstand wisselt:
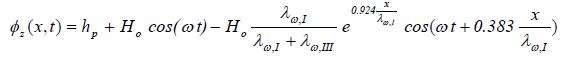 A(1.15)
A(1.15)
-
en in gebied III:
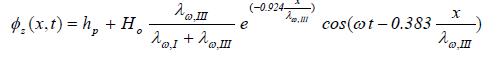 A(1.16)
A(1.16)
Hierin zijn λω,I en λω,III de spreidingslengtes die horen bij het cyclische probleem. Deze zijn een functie van de spreidingslengtes voor de stationaire situatie, λIen λIII(formules A(1.3) en A(1.4)), de hydrodynamische perioden van de deklagen, th,Ien th,III, en de hoeksnelheid ω:
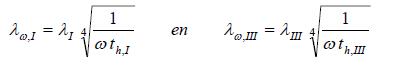 A(1.17)
A(1.17)
We zien dat, voor hydrodynamische perioden van de deklagen die groot zijn ten opzichte van de periode waarmee de buitenwaterstand wisselt, de cyclische spreidingslengtes aanzienlijk kleiner zullen zijn dan in de stationaire situatie. Dit betekent dat het gebied in de zandlaag, waarin de stijghoogte vervalt van buitenwaterstandniveau tot polderpeil aanzienlijk kleiner is dan in het stationaire geval (zie ook Figuur 5.8 in de hoofdtekst).
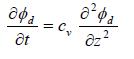 A(1.10)
A(1.10)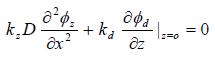 A(1.11)
A(1.11)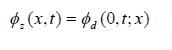 A(1.12)
A(1.12)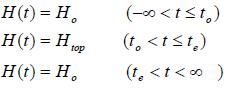 A(1.13)
A(1.13)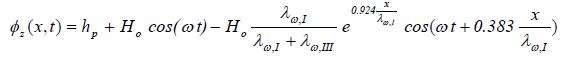 A(1.15)
A(1.15)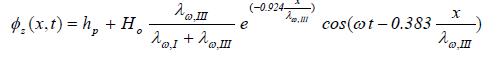 A(1.16)
A(1.16)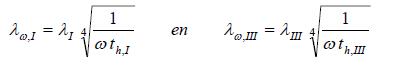 A(1.17)
A(1.17)