Golven - Hydraulische belastingen

Golven

Algemeen

Bij het waarnemen van windgolven nabij een waterkering valt enerzijds een zekere regel- matigheid en anderzijds een zekere grilligheid op. Beide aspecten vindt men terug in de beschrijving van golven. Golven worden voorgesteld als een periodieke beweging, te karak- teriseren met een golfhoogteH (de afstand tussen top en dal), een golfperiode T (de tijd tussen het passeren van twee opeenvolgende neergaande nuldoorgangen), een golflengte L (de horizontale afstand tussen twee opeenvolgende neergaande nuldoorgangen), en een golfrichting θ. Vervolgens wordt een meer realistische voorstelling verkregen door het golfbeeld voor te stellen als een samenstelling van een groot aantal componenten met elk een eigen waarde voor H en T en θ. In zijn eenvoudigste vorm wordt zo’n onregelmatig golfbeeld beschreven met twee nieuwe parameters, bijvoorbeeld de significante golfhoogte Hsen de significante golfperiode Ts, die redelijk aansluiten bij de golfhoogte en golfperiode zoals die van oudsher door zeelieden werden geschat. Hsis per definitie gelijk aan het gemiddelde van het hoogste één-derde deel van de golven. Evenzo is dan Tshet gemiddelde van het hoogste één-derde deel van de golfperiodes.

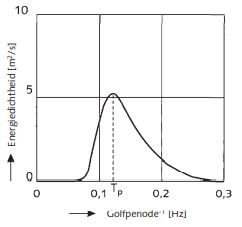
Een andere mogelijkheid om golfvelden te analyseren is met behulp van spectrale analyse. Het golfveld wordt hierbij beschouwd als zijnde opgebouwd uit verschillende sinusgolven, ieder met een hoogte en periode. De analyse resulteert in een golfspectrum; dit geeft de verdeling van de energie weer over de frequenties. De frequenties zijn de in het golfveld aanwezige golfperiodes, en de energie is een maat voor de golfhoogte die bij die frequentie hoort. Uit dit spectrum zijn karakteristieke maten te halen voor de golfhoogte en golfpe- riode (en golfrichting). Veel gebruikt worden Hm0 (spectrale significante golfhoogte), Tm01 (spectrale gemiddelde periode) en Tp(piekperiode). In de golfoverslagberekeningen is Tm-1,0 benodigd (zie paragraaf 7.3.2). De reden hiervoor is dat de Tpvoor golfspectra na sterke breking of bij meer toppen niet goed te bepalen is.

Opgemerkt wordt dat golven in een golfveld ook verschillende richtingen hebben; ook deze kunnen spectraal geanalyseerd en beschreven worden. In Figuur 7.3 is een vereenvoudigd golfspectrum weergegeven, overgenomen uit Technisch Rapport Steenzettingen (TAW, 2003).

In Figuur 7.3 is een vereenvoudigd golfspectrum weergegeven, overgenomen uit Technisch Rapport Steenzettingen (TAW, 2003).

Figuur 7.3 Voorbeeld vereenvoudigd golfspectrum

Golfberekeningsmethoden

Voor de bepaling van golfhoogte en golfperiode uit windgegevens zijn verschillende metho- den beschikbaar. Van eenvoudig naar complex zijn dit:

1. golfgroeiformules

Golfgroeiformules geven een eenvoudig verband tussen een karakteristieke golfmaat en windsnelheid, strijklengte en waterdiepte. In Holthuijsen (1980) is een overzicht gegeven van verschillende golfgroeikrommes. De bekendste is van Bretschneider (1973). Andere golfgroeikrommes zijn die van Wilson (1965). Recenter onderzoek heeft nog andere krom- mes opgeleverd, zoals die van Kahma en Calkoen (1992) voor diep water en Young en Verhagen (1996).

2. geparametriseerd golfmodel zoals HISWA

Het golfmodel HISWA is door de TU Delft ontwikkeld aan het eind van de jaren tachtig van de vorige eeuw (Holthuijsen et al., 1989). Het rekent stationair op een tweedimensionaal grid en karakteriseert het golfveld door karakteristieke golfparameters per golfrichting. Per golfrichting wordt de totale golfenergie, en de gemiddelde golfperiode beschouwd. Het houdt rekening met golfgroei, voortplanting, breking, bodemwrijving, refractie en shoa- ling. Voor het Haringvliet en Hollandsch Diep is een HISWA-model ontwikkeld (Veldman en Hurdle, 1997). Inmiddels is het model verouderd en opgevolgd door het golfmodel SWAN.

3. volledig spectraal golfmodel zoals SWAN

SWAN (Ris, 1997) is een volledig spectraal model, wat betekent dat elke golffrequentie en golfrichting apart gemodelleerd worden. Evenals HISWA, is het model SWAN ook ontwik- keld door TU Delft. Er wordt rekening gehouden met dezelfde processen als in het model HISWA, alleen worden deze processen op basis van betere fysica gemodelleerd. Ook wordt rekening gehouden met de onderlinge interacties tussen de golfcomponenten. Het grote voordeel van SWAN is dat alle golfcomponenten in een golfveld worden gemodelleerd. Fysische processen zijn gebaseerd op theoretisch dan wel op experimenteel onderzoek. Uit vergelijking met metingen blijkt dat de golfhoogte over het algemeen goed berekend wordt, maar dat de golfperiode wat wordt onderschat.

Toepassing golfmodellen voor rivieren

Door het ontbreken van voldoende waarnemingen van golfhoogten en golfperioden op de rivier is het niet mogelijk om aan te geven in welke mate de werkelijke golfaanval bij stromend water in de rivier zal afwijken van de berekende waarde; die geldt namelijk in het algemeen voor niet-stromend water. Er is nog veel onbekend over golfgroei in aanwezig- heid van stroming.

Voor een gedeelte van de Waal is onderzocht wat de meerwaarde is van toepassing van golfmodellen HISWA en SWAN ten opzichte van Bretschneider (Beyer et al., 2000). Daaruit bleek dat bij verwaarlozing van de stroming tijdens maatgevende omstandigheden de golfhoogtes en golfperiodes van de drie methodes elkaar niet veel ontliepen. Bretschneider kwam qua golfhoogte wat hoger uit, terwijl de piekperiode vergelijkbaar of lager was. De golfoploop (berekend op een standaard talud) kwam voor de drie methodes vergelijkbaar uit. Voor locaties met een waterdiepte kleiner dan 1,5 à 2 m kan een golfmodel wel meer- waarde hebben omdat refractie en breking belangrijker worden.

Op grond van de voorgaande vergelijking en het gebrek aan kennis over golfgroei op rivie- ren wordt het volgende aanbevolen:

• Op de bovenrivieren en de smalle wateren in de benedenrivieren en de IJssel- en Vechtdelta wordt aanbevolen de eenvoudige golfgroeiformules toe te passen. Deze formules geven een redelijke schatting van de golfhoogte en golfperiode en worden in Bijlage E toegelicht. In deze bijlage wordt tevens ingegaan op de invloed van vegetatie, obstakels, voorlanden, havens en complexe situaties;
• Op de brede wateren van het Haringvliet, Hollandsch Diep en de Biesbosch wordt aanbevolen om het 2D-golfmodel SWAN te gebruiken. Het is aan te bevelen om de berekeningen met SWAN door specialisten uit te laten voeren. Het maken van 2D-bere- keningen vergt echter veel rekentijd en het is daarom niet realistisch te verwachten dat deze voor alle duizenden belastingcombinaties gemaakt kunnen worden. Voorlopig is er echter geen gevalideerd model beschikbaar. Tot die tijd kan gebruik worden gemaakt van golfgroeiformules. Daarbij dient bedacht te worden dat dit een benadering is en dat de geometrie eigenlijk te complex is voor het gebruik van golfgroei- formules. In paragraaf E.5 van Bijlage E worden hierover enkele opmerkingen gemaakt. Om een indruk te krijgen van de nauwkeurigheid wordt aanbevolen enkele controlebere- keningen te (laten) maken met SWAN.

Voor achtergronden en beperkingen wordt verwezen naar paragraaf 11.3.