Copy of Berekeningsmodellen - Waterspanningen en styghoogten

1. 1. Grafische benadering

Bij twee-dimensionale quasi-stationaire grondwaterstroming door een isotroop door­ latend grondmassief kan het stromingsbeeld worden benaderd door gebruik te maken van de eigenschap dat stroomlijnen en potentiaallijnen een orthogonaal stelsel vormen: de vierkantennet-methode.

Worden potentiaallijnen <Pi. <P2, <P3 .... met interval !!.<P en stroomlijnen 'Pi. 'P2, 'P3 •••• met interval !::.. 'P getekend, dan geldt bij benadering

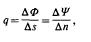
waarbij !!.s de afstand tussen twee potentiaallijnen is, en An de afstand tussen twee stroomlijnen (lit. 34, 43).

Wordt nu A <P =A 'P gekozen, dan geldt bij benadering As= An.

Met andere woorden, de onderlinge afstand van potentiaallijnen en stroomlijnen is in elk punt ongeveer gelijk; de stroomlijnen en potentiaallijnen vormen elementaire, ge­ kromde vierkantjes.

Een goed vierkantennet moet aan de volgende eisen voldoen:

I. potentiaallijnen en stroomlijnen zijn overal orthogonaal;

1. potentiaallijnen en stroomlijnen vormen overal vierkantjes - dit is te controleren door de diagonalen te tekenen: die moeten ook orthogonaal zijn;

2. het net sluit aan op de randvoorwaarden.

Een dergelijk vierkantennet laat zich in veel gevallen eenvoudig schetsen. Figuur 10.6 is een illustratie die betrekking heeft op de stroming door een zandlaag onder een klei­ dijk.

In het voltooide net kan men overal de potentiaal bepalen en dus ook de stijghoogte rp = <P/ k, en de waterspanning u = (rp - z) Q g, omdat nu het interval Arp bekend is. Arp volgt namelijk uit ·(rp1 - rp0)/a, waarin a het aantal vierkantjes per stroombaan is. Het debiet per stroombaan AQ =A 'P = A <P.

112

Het totale debiet, onder de constructie door, volgt dan uit bet totale aantal (b) gecon­ strueerde stroombanen: Q = bll.Q.

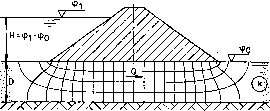
figuur 10.6

De grafiscbe metbode kan ook worden toegepast op problemen met een vrije grond­ waterspiegel. Hierbij treedt een extra moeilijkbeid op, doordat de positie van bet vrije oppervlak, <lat ook een stroomlijn is, onbekend is. Langs bet vrije oppervlak geldt als twee de randvoorwaarde dat de druk u in bet water er nul moet zij n als de capillaire op­ stijging verwaarloosd wordt. Dit betekent dat rp = z.

Het onderste gedeelte van bet binnentalud, waar water uittreedt, vormt bet zogenaam­ de kweloppervlak. Het water treedt daar uit en stroomt langs bet talud naar beneden. Langs bet kweloppervlak moet ook gelden rp = z.

Een voorbeeld van een voltooid vierkantennet voor de stroming door een dijk geeft figuur 10.7.

'

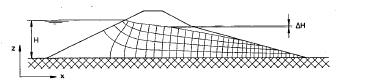
figuur 10.7

De controle van de conditie rp = z langs bet vrije oppervlak en bet kweloppervlak gaat bet eenvoudigst door bet boogteverscbil ll.Htussen de snijpunten van deze randen met twee opvolgende potentiaallij nen te bepalen: dit moet voor elk tweeta! opvolgende snij­ punten betzelfde zijn.

Wil men we! rekening bouden met capillaire opstijging, dan is eenzelfde procedure

mogelijk. Voor de Jigging van de freatiscbe lijn geldt z= rp, en voor bet vrije oppervlak

z= rp +he, waarin he de capillaire opstijging is.