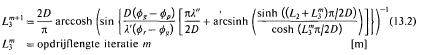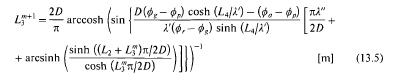B. Opdrijflengte bij stationaire stroming
[m]
In figuur 13.2 wordt het geologisch profiel schematisch weergegeven, waarbij in een zone met breedte L3achter de dijk opd rijven optreedt (lit. 3).
169
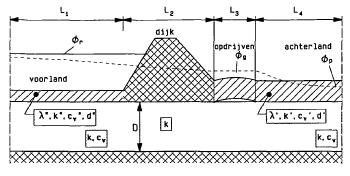
figuu r B 13.2
De verklaring van de variabelen in figuur Bl3.2 l uidt:

De omgeving van de dijk wordt in 4 zones verdeeld:
-
het voorland, met breedte l1
-
de dijk met berm, met breedte l 2
-
de opd rijfzone, met breedte l 3
-
het achterland, met breedte l 4
Het achterland kan 'oneindig' uitgestrekt (meerdere km's) zijn, dan we! begrensd va n lengte, bijvoorbeeld in het geval van een kanaal, een zandwin plas dan we! een zeer dun klei/veen-dek op enige afstand van de dijk.
De lengte van de opdrijfzone (L3) kan voor een stationaire stroming met oneindig achterland nu worden bepaald met behul p van de formule (13.2):
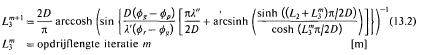
De formule werkt iteratief. Meestal zijn slechts enkele iteraties voldoende om een nauwkeu rig waarde voor l 3 te vinden. Bovenstaande formule is eenvoudig te pro grammeren.
170
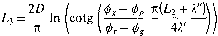
Voor het geval L3 < D < L2 volgt een eenvoudiger formule:
[m) (13.3)
Voor een situatie zonder voorland geldt bovenstaande formule met ).'' = 0.
Een kritieke potentiaal, waarbij nog net L3 = 0 geldt, en er nog net geen opdrijven plaatsvind t luidt:
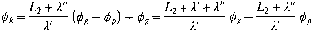 [m) (13.4)
[m) (13.4)
Bovenstaande formule voor L3 is geldig voor een dun kleidek op het voorland, waarbij dus ). is klein.
Voor het geval van een eindig voorland met een dik klei pakket moet voor de term ). worden gesubstitueerd:
). tanh ( Li / ). ), waarin Li is de voorlandbreedte. Voor ). >>Li gaat deze vorm dan over in Li .
Voor het geval het achterland een eindige lengte L4heeft, waar een potentiaal ¢0aan wezig is, wordt de breedte van de opdrijfzone bepaald met behulp van de iteratieve formule:
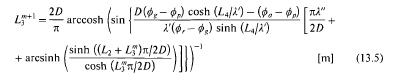
Ook in deze formule moet bij een begrensd voorland ). worden vervangen door
). tanh (l'i/ ).'').