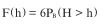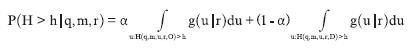Basisformules probabilistisch model - Bijlage D Probabilistisch model van de IJssel- en Vechtdelta

Basisformules probabilistisch model

Blokkansen

De kleinste tijdschaal in het model Hydra-VIJ is een periode van 12 uur; kansen gerelateerd aan deze periode worden ‘blokkansen’ genoemd (analoog aan het begrip ‘getijkans’ uit Hydra-B). Aanname in Hydra-VIJ is dat elke 12 uur, onafhankelijk van de voorafgaande 12- uursperiode, sprake kan zijn van een andere windsnelheid en windrichting. Bij een gegeven 12-uursperiode wordt met P(H>h|q,m,r) de blokkans aangegeven dat in deze periode belastingniveau h wordt overschreden, bij gegeven afvoer q, meerpeil m en windrichting r. De formule hiervoor luidt:

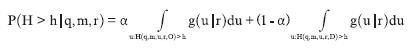
2 Overigens zijn f(k) en f(s) beslist niet gelijk aan de werklijnen voor de afvoer en het meerpeil.

Hierin geeft g(u|r) de kansdichtheid van het 12-uursmaximum van de windsnelheid, gege- ven richting r (zie voor meer informatie over g(u|r) verderop), terwijl α de faalkans van de Ramspolkering voorstelt (gelijk aan 0.0035 per sluitvraag). De gegeven formule oogt in eerste instantie plausibel. Er is een kans α dat de kering faalt en een kans 1 - α dat de kering juist functioneert, in welke gevallen we respectievelijk uitgaan van de belastingen voor de open en dichte keringssituatie. De integraties worden uitgevoerd over díe windsnelheden waarvoor H het niveau h overschrijdt. De factoren α en 1 - α geven dan de juiste weging over de situaties van open en dichte keringen. In tweede instantie is de formule misschien minder plausibel. Er zijn namelijk situaties q,m,u,r waarin het sluitingscriterium niet wordt gehaald, in welk geval de faalkans α geen enkele rol speelt; deze situaties lijken niet voor te komen in de formule. In Geerse (2003) wordt aangetoond dat de formule wel degelijk correct is, en dat de vorm van de formule het gevolg is van het feit dat voor situaties waarin het sluitcriterium niet wordt gehaald de belastingen voor de open en dichte situatie over- eenstemmen.

Bij een gegeven 12-uursperiode wordt met P(H>h|q,m) de blokkans aangegeven dat in deze periode belastingniveau h wordt overschreden, bij gegeven afvoer q en meerpeil m. De formule hiervooor kan verkregen worden door in de formule voor P(H>h|q,m,r) te ver- menigvuldigen met de kans P(r) op richting r, en vervolgens te sommeren over de moge- lijke richtingen:

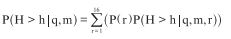
Trapeziumkansen

De zojuist genoemde blokkans kan worden aangewend om de kans op overschrijden van niveau h te berekenen gedurende de basisduur B = 30 dagen. Kansen gerelateerd aan duur B worden ‘trapeziumkansen’ genoemd. Het doel van deze paragraaf is om de kans PB(h) te bepalen, zijnde de kans dat gedurende duur B een overschrijding van niveau h plaatsvindt.

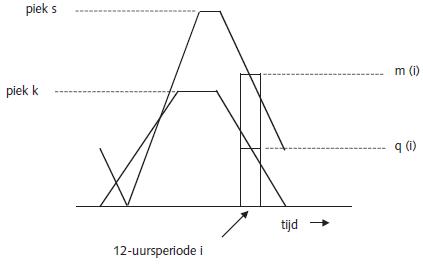
Beschouw daartoe eerst in basisduur B een gegeven afvoertrapezium met piekwaarde k en een gegeven meerpeiltrapezium met piekwaarde s, zie Figuur D.2. Deel deze trapezia op in n(B) = 60 12-uursblokken, en geef de gemiddelde afvoer in blok i aan met q(i) en het gemiddelde meerpeil met m(i). De kans op geen overschrijding van niveau h in blok i is dan 1-P(H>h|q(i),m(i)). De kans dat gedurende de hele duur B geen overschrijding van niveau h optreedt, is dan gelijk aan het produkt van alle kansen 1-P(H>h|q(i),m(i)), i = 1 t/m 60. De kans dat, bij gegeven trapezium-piekwaarden k en s dan wel een overschrijding van niveau h optreedt gedurende duur B, is dan

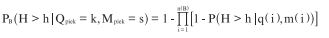
De ‘volledige’ kans op een overschrijding van niveau h gedurende duur B volgt dan door de piekwaarden k en s uit te integreren:

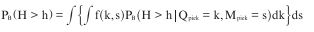
waarbij de integratie over alle mogelijke waarden voor k en s plaatsvindt.

Figuur D 2 Afvoer- en meerpeiltrapezium met 12-uursperiode i

Overschrijdingsfrequentie winterhalfjaar

Bij een vast beschouwde basisduur B geeft PB(h) de kans dat gedurende duur B een over- schrijding van niveau h plaatsvindt. Omdat het winterhalfjaar is gevuld met 6 basisduren, volgt de overschrijdingsfrequentie van niveau h, in keren per jaar, dan simpelweg door PB(h) met 6 te vermenigvuldigen: