Afschuiven binnentalud door overslag - Onderzoek en berekeningen

Bij overslag stroomt er water over de kruin van een dijk langs het binnenta­lud. Dit water infiltreert in het grondlichaam, zie figuur I. Bij voldoende overslag zal de grond na zekere tijd verzadigen. Door de toename van de waterspanning neemt de korrelspanning af. Als de helling vrij steil is, bezwijkt de grond, omdat de verhouding tussen de schuifspanning en de normaalspan­ ning groter wordt dan de grond kan mobiliseren. Dit leidt tot het afschuiven van het binnentalud.

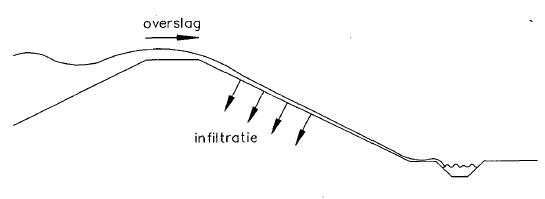
Figuur I. Overslag en infiltratie

Bij de watersnoodramp van 1953 zijn veel Zeeuwse dijken hierdoor bezweken. Het afschuiven van het binnentalud door overslag is eveneens waargeno­men bij een proef op schaal I : I uitgevoerd door het 'Kystinspektoratet' in Denemarken. 27

In aansluiting op Leidraad I, paragraaf I 1.4 wordt in deze paragraaf besproken hoe kan worden nagegaan of afschuiven van het binnentalud kan optreden door infiltratie ten gevolge van overslag. Onderstaand is de methode beschreven hoe bij de constructie rekening kan worden gehouden met infiltratie ten gevolge van overslag. Een beschrijving van de fysische mechanismen is gegeven in bijlage 2, hoofdstuk 2.E, waar ook meer gedetailleerde informatie en randvoorwaarden zijn gegeven.

Belangrijke aspecten bij infiltratie ten gevolge van overslag als bezwijkrnechanisme zijn het overslagdebiet, de helling van het binnentalud en de opbouw van de dijk.

Bij een overslagdebiet gelijk of kleiner dan 0, I l/m/s, mag worden aangenomen dat niet voldoende infiltratie kan optreden om een verhoogde water­ spanning in een potentieel glijvlak te doen ontstaan.

Wat de opbouw van de dijk betreft, kunnen twee karakteristieke situaties worden bezien:

I de dijk is geheel uit klei opgebouwd

2 de dijk heeft een zandige kern en een kleiige toplaag.

Ad I

De klei aan het oppervlak is veel doorlatender dan de klei in de kern. Scheurtjes en wortelkanalen creeren een voor klei vrij hoge doorlatend­heid van de orde van 10^-5 tot 10^-4 m/s. Bij overslag infiltreert water juist het sterkst in de toplaag, waardoor de waterspanning oploopt. De korrelspanning neemt hierdoor uiteindelijk zoveel af, dat een glijvlak kan ontstaan op de grens van toplaag en kern op een diepte van orde Im onder het maaiveld. Bij een te steil talud schuift de toplaag af.

Ad 2

Ook bij een dijk met een zandige kern kan infiltratie de oorzaak van het bezwijken door overslag zijn. De doorlatendheid van de toplaag is sterk anisotroop. Door scheurtjes en begroeiing is de doorlatendheid van de toplaag vaak maar weinig minder dan die van de kern. In de richting lood­recht op het talud is de doorlatendheidswaarde veel groter dan in de richting langs het talud. Door deze anisotropie stroomt er relatief weinig water door de toplaag evenwijdig aan het talud, het meeste zakt de zandige kern in. Als de kern niet is gedraineerd en verzadigd raakt met water, kan aan de teen een overdruk onder de toplaag ontstaan. Deze kan de toplaag oplichten, waarna de toplaag langs het talud naar beneden schuift. Er treedt een glijvlak op in de directe nabijheid van het scheidingsvlak tussen de kern en de kleiige toplaag.

Voor de dimensionering zijn er verschillende technieken beschikbaar: analytische en numerieke methoden. Als analytische methode kan voor een homogeen oneindig lang talud de methode van Joustra en Edelman worden gebruikt, die overeenkomt met die van de Leidraad I, paragraaf 11.4.2.

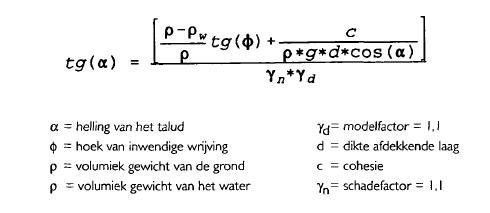
Voor steile taluds is de cohesie essentieel. Helaas is de waarde ervan voor grond in de toplaag moeilijk vast te stellen vanwege de lage spanning.

Deze formule levert een tamelijk conservatief resultaat op, omdat deze uitgaat van een oneindig lang talud. Extra steundruk ten gevolge van de aanwe­ zigheid van de teen wordt daarom niet verdisconteerd in de korrelspanning. Deze extra steundruk speelt geen rol als de toplaag aan de onderzijde van het talud wordt afgedrukt. Bovendien wordt een tamelijk ongunstige stijghoogteverdeling aangenomen. Anderzijds leidt de formule mogelijk tot acceptatie van te steile taluds in gevallen waarbij de spanning evenwijdig aan het talud relatief gering is.

Een juist inzicht in de spanningsverdeling in de toplaag ontbreekt nog.

De eenvoudigste numerieke methode is een glijvlakberekening met de methode van Bishop (Leidraad I, paragraaf I 1.3.1). Het glijvlak is cirkelvor­mig. Net als bij bovenstaande formule, kan worden aangenomen dat het freatisch vlak samenvalt met het talud en dat de stijghoogte constant is langs lijnen loodrecht op het talud. Bij een zandige kern zal de stijghoogte verdeling veelal veel gunstiger zijn. Men kan die verdeling vaststellen met een grondwaterstromingsberekening.

Met behulp van eindige elementen methoden kan het grondgedrag nog beter worden gemodelleerd, omdat de vorm van het glijvlak niet a priori vastligt, zoals bij de methode van Bishop. In paragraaf 3.2 wordt de dimensionering verder uitgewerkt.