Probabilistische ontwerpprocedure - Bijlagen

Probabilistische ontwerpprocedure

Inleiding

Op basis van de in de Appendix F beschreven theorie en de beschreven spreadsheet- modellen is een reken- en ontwerpprocedure uitgewerkt. De procedure heeft tot doel geotechnische constructies te ontwerpen op een vooraf vastgelegd betrouwbaarheids- niveau voor bezwijken. De procedure geldt voor een niet-homogene ongedraineerde grondslag en is uitgewerkt voor kistdammen. De procedure kan ook worden toegepast voor diepwanden en andere geotechnische constructies.

In de procedure wordt ook gebruik gemaakt van het PLAXIS eindige elementen programma. Daarbij is uitgegaan van de in PLAXIS 5.1 aanwezige mogelijkheden. Daarnaast wordt gebruik gemaakt van de in Appendix F beschreven spreadsheet- modellen. Voordat de procedure kan worden toegepast moet worden bepaald of de constructie zich wel ongedraineerd zal gedragen. Voor gedraineerde constructies kan de procedure niet zonder voorbehoud worden toegepast.

Stap 1 Vaststellen uitgangsgegevens

Bepaal de volgende gegevens:

• globale geometrie
• grondopbouw
• uitwendige belasting
• grondparameters, per grondlaag:
  • volumiek gewicht
  • elasticiteitsmodules
  • dwarscontractiecoëfficiënt
  • dilatantiehoek Ψ(voor klei en veen geldt Ψ= 0)
  • cohesie µ (c’) (= ca) en standaardafwijking σ(c’)
  • hoek van inwendige wrijving µ(φ’) (= φa) en standaardafwijking σ((φ’)
  • wandwrijvingscoëfficiënt µ (Rw) en standaardafwijking σ (Rw)
• laagscheidingen, per laagscheidingsniveau:
  • gemiddelde ligging µ(s) en standaardafwijking σ(s)
• damwand en ankerparameters, per toegepaste materiaalsoort:
  • elasticiteitsmodules E
  • gemiddelde breuksterkte of vloeigrens µ(ƒy) en standaardafwijking σ((ƒy)
• grondwaterregiem
• verloop van grondwaterregiem in de tijd
• bouwfaseringen, inclusief te verwijderen en/of aan te brengen grond.

Stap 2 Betrouwbaarheidsniveaus en faalkansen bepalen

• Bepaal het gewenste betrouwbaarheidsniveau βk van de kistdam.
• Bepaal uit βk de faalkansruimte Pƒk.
• Deel de faalkansruimte Pƒkzo op in faalkansen Pƒg, Pƒd;l, Pƒd;ren Pƒavoor respectie- velijk grondmechanisch bezwijken, damwandbreuk links, damwandbreuk rechts en ankerbreuk dat voor ieder van de damwanden wordt voldaan aan de volgende ongelijkheden:

Pƒa ≤Pƒd;i

Pƒg ≤Pƒd;i

waarin i = links of rechts.

Bij voorkeur moet de faalkansruimte zo worden opgedeeld dat ook aan de volgende ongelijkheid wordt voldaan:

Pƒa ≤Pƒg ≤Pƒd;i

Bepaal uit Pƒg, Pƒd;i, Pƒd;r, Pƒa de betrouwbaarheidsniveaus βg, βd;l, βd;r, βa.

Noot 2.1

De in stap 2 aangegeven procedure heeft tot gevolg dat de betrouwbaarheidsniveaus bg, βd;l, βd;r, βa altijd groter zijn dan het betrouwbaarheidsniveau βk van de kistdam.

Noot 2.2

In termen van betrouwbaarheidsniveaus resulteren de eerste twee ongelijkheden in:

bd;i ≤ ba

bd;i ≤ bg

De derde ongelijkheid resulteert in:

bd;i ≤ bg ≤ ba

Eerste ongelijkheid

Het aan het anker toekennen van een grotere betrouwbaarheid dan aan de damwanden heeft tot gevolg dat de betrouwbaarheid van de damwanden kleiner kan worden. Omdat ankers goedkoop zijn en de damwanden duur resulteert dit in een meer economisch ontwerp.

Tweede ongelijkheid

Het aan de grond toekennen van een grotere betrouwbaarheid dan aan de damwanden heeft tot gevolg dat de damwanden verder moeten worden doorgezet en/of de breedte van de kistdam moet toenemen om de vereiste stabiliteitsfactor te bereiken.

Net als bij gewone verankerde damwanden heeft dit een inklemmingsmoment tot gevolg, hetgeen resulteert in een meer economisch ontwerp.

Derde ongelijkheid

Het aan de grond toekennen van een nog grotere betrouwbaarheid dan aan het anker kan wel, maar heeft waarschijnlijk weinig nut. Dat de gunstiger krachtsverdeling zou bijdragen aan een meer economisch ontwerp gaat niet op, omdat ankers toch goedkoop zijn.

Anderszins is het maar de vraag of de nog gunstiger krachtverdeling wel opweegt tegen de grotere inheidiepte en/of breedte van de kistdam die nodig zijn om aan het betrouw- baarheidsniveau voor grondmechanisch bezwijken te voldoen.

Noot 2.3

Bij een ander soort constructie als een kistdam kan voor het opdelen van de faalkans- ruimte dezelfde procedure worden toegepast. Het verschil is dat in dat geval de totale faalkansruimte anders moet worden verdeeld over de verschillende bezwijkmechanismen.

Stap 3 Veiligheidsfactor schatten

• Schat de veiligheidsfactor Σ − MSFc(=Fv,c ) die de constructie moet hebben om aan het betrouwbaarheidsniveau βg voor grondmechanisch bezwijken te voldoen.

Noot 3.1

Geadviseerd wordt om, afhankelijk van het betrouwbaarheidsniveau voor grondbreuk, als eerste schatting een Σ −MSFc tussen de 1,25 en 1,50 aan te houden.

Als richtlijn: door GeoDelft is een verificatieberekening uitgevoerd voor een twee-lagen kistdam; voor een betrouwbaarheidsniveau van de hele kistdam

βg = 3,88 volgde een benodigde Σ −MSF = 1,38.

• Bepaal met enkele PLAXIS berekeningen met φ’/c’-reductie een zodanige geometrie van de kistdam dat de constructie ongeveer bij de hiervoor bepaalde Σ −MSF bezwijkt.

In deze berekeningen moeten de initiële gedraineerde spanningen worden aangebracht met voor alle grondlagen de c’c en φ’c die behoren bij de vooraf geschatte eindwaarde van Σ −MSFc. Aan het begin van het ongedraineerd belasten moeten weer gemiddelde waarden c’a en φ’a worden ingevoerd. De waarden van c’cen φ’c volgen uit:

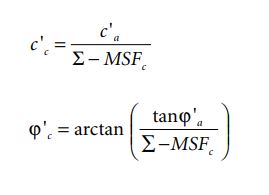
Noot 3.2

Bij PLAXIS berekeningen met φ’/c’-reductie is het soms lastig om een eenduidige waarde voor Σ −MSFcte bepalen. Aanbevolen wordt om de berekening door te zetten tot een stabiel bezwijkmechanisme is ontstaan en de global error van PLAXIS klein is (orde 10-4à 10-6). Voor Σ −MSFckan dan het gemiddelde van het laatste deel van de curve Σ −MSFcworden aangehouden.

Noot 3.3

De berekeningen verlopen het snelst als hoge stijfheden voor ankers en damwanden worden ingevoerd. Aanbevolen wordt om de stijfheden een factor 10 te groot nemen.

Stap 4 Bezwijkmechanisme en kinematische elementen bepalen

• Bepaal voor de in stap 3 ( of de laatste in 8) uitgevoerde PLAXIS berekening de “incremental displacements” na φ’/c’-reductie. Deze incremental displacements worden in het vervolg aangeduid als “het bezwijkmechanisme”. De grootte van de incremental displacements worden in het vervolg aangeduid als “de verplaatsingen”.
• Bepaal uitgaande van het bezwijkmechanisme een systeem van kinematische elementen waarmee het bezwijkmechanisme zo goed mogelijk kan worden beschreven. Voor de kinematische elementen kan worden gekozen uit:
  • Grondelementen
  • Schuifvlakelementen
  • Wandwrijvingselementen

Noot 4.1

Het systeem van kinematische elementen moet zo worden bepaald dat de laagschei- dingen altijd op de randen van de elementen liggen. De indeling wordt verder bepaald door de ligging van de buitenranden van het bezwijkmechanisme en de plaats van de damwanden.

Noot 4.2

Bij de indeling in kinematische elementen moet er voor worden gezorgd dat de verplaat- singen binnen de elementen zoveel mogelijk lineair verlopen. Dit betekent dat bij sterk niet-lineair verlopende vervormingsgradiënten binnen één grondlaag meerdere elementen noodzakelijk kunnen zijn.

Noot 4.3

Bijvoorbeeld links en rechts van de teen van een damwand kunnen schuifvlakken voorkomen. Dit zijn relatief smalle plastische zones met relatief grote afschuifvervor- mingen.

In de schuifvlakken kunnen behalve afschuivingen ook verplaatsingen loodrecht op het afschuifvlak optreden. De schuifvlakken kunnen worden beschouwd als grondelementen met een dikte van bijvoorbeeld 0,10 m.

• Bepaal voor alle kinematische elementen per kinematisch element een zo goed mogelijk linearisatie van de verplaatsingen binnen het kinematisch element en op basis hiervan verplaatsingen van de hoekpunten.

Noot 4.4

De linearisatie van de verplaatsingen binnen de kinematische elementen kan tot gevolg hebben dat de verplaatsingen van de hoekpunten niet meer gelijk zijn aan de in de PLAXIS berekende verplaatsingen. Ook kan dit betekenen dat verplaatsingen van gemeenschappelijke hoekpunten van kinematische elementen niet meer gelijk zijn, zodat het systeem van kinematische elementen strikt genomen niet meer zuiver kinema- tisch is.