Rekenmodelonzekerheidsfactoren
Modelonzekerheidsfactoren verdisconteren zowel onnauwkeurigheden (beperkingen) van de rekenmethode zelf, als onnauwkeurigheden die het gevolg zijn van schema- tiseringuitgangspunten. Met dit laatste wordt bedoeld dat een tweedimensionaal rekenmodel wordt gebruikt om een driedimensionaal verschijnsel (een afschuiving) te beschrijven. Bij dit laatste wordt onderscheid gemaakt tussen ‘opdrijfsituaties’ en situaties waarbij opdrijven geen rol speelt (‘niet opdrijfsituaties’). De rekenmodel- onzekerheidsfactor bestaat daarom uit twee deelfactoren voor de genoemde aspecten.
Bij het herijken van de materiaal- en schadefactoren voor stabiliteitsanalyses ten behoeve van de Leidraad Rivieren [6] is mogelijke aanpassing van de modelonzeker- heidsfactoren in het TRWG niet overwogen. Wel is, sinds het uitkomen van het TRWG de methode voor stabiliteitsanalyse bij opdrijven van de binnendijkse deklaag veranderd. De oude ‘drukstaaf analyse’ is vervallen en vervangen door de methode LiftVan11[28]. Dit bracht ook een verandering van de aan te houden rekenmodel- onzekerheidsfactor met zich mee. In de oorspronkelijke opzet werden model- onzekerheidsfactoren gekoppeld aan het type rekenmodel, namelijk glijcirkel ana- lyses volgens de Bishop methode, afschuifanalyses met behulp van een eindige elementenmethode (Plaxis) en gecombineerde glijcirkel/glijvlakanalyses volgens LiftVan. Differentiatie van de modelonzekerheidsfactoren was zowel gebaseerd op verschillen tussen de rekenmethoden als op situatie waarop de berekening wordt toegepast, namelijk wel of geen opdrijfsituatie.
Ten aanzien van de rekenmethodeis het argument voor differentiatie dat, naarmate de methoden minder beperkingen hebben ten aanzien van potentiële afschuifvormen en de evenwichtsanalyse vollediger is, de modelonzekerheid kleiner is. Zo zijn bij een Bishop-analyse de afschuifvormen beperkt tot glijcirkels en bestaat de even- wichtsanalyses uit globaal momentenevenwicht van de afschuivende grond. Bij toepassing van een eindige elementenmethode (PLAXIS) wordt, in principe, geen bezwijkvorm opgelegd, maar volgt deze uit evenwichtsbeschouwingen overal binnen het grondmassief. De methode LiftVan zit hiertussen. Daarbij wordt de afschuifmode gevormd door twee cirkelbogen met daartussen een horizontaal vlak. Net als de methode van Bishop, wordt hierbij gekeken naar globaal momenten- evenwicht van beide afschuivende glijcirkels afzonderlijk en de horizontale interactie- krachten tussen cirkels en het horizontale gedeelte van de afschuifmode. In het uiterste geval kan de lengte van het horizontale gedeelte van de afschuifmode tot nul teruglopen, waarbij de twee cirkelbogen aan elkaar aansluiten. Als vervolgens de cirkelbogen eenzelfde rotatiemiddelpunt hebben, is de methode LiftVan identiek aan de methode Bishop. Met andere woorden, de mogelijke afschuifvormen die onderzocht worden bij de methode LiftVan sluiten de mogelijke afschuifvormen die onderzocht worden bij de methode Bishop volledig in, maar deze vormen een beperkte deelverzameling.
De deelfactor voor de rekenmethode is groter, naarmate het bereik aan potentiële afschuifvormen kleiner is (zie tabel A.3).
Ten aanzien van de schematisering (2D rekenmodel voor 3D situatie) geldt het volgende. In het 2D rekenmodel worden voor de taludstabiliteit gunstige rand- of scholeffecten genegeerd. Die effecten zijn in situaties zonder opdrijven van de
11 De methode LiftVan was oorspronkelijk bedoeld voor opdrijfsituaties, maar is inmiddels ook geschikt gemaakt voor situaties waarin opdrijven geen rol speelt (inclusief ondiepe glijvlakken)
binnendijkse deklaag relatief groter dan in situaties met opdrijven. Om die reden wordt voor de deelfactor ten aanzien van de schematisering onderscheid gemaakt tussen deze twee situaties.
De voorgestelde deelfactoren en de daaruit volgende totale rekenmodelonzeker- heidsfactoren zijn weergegeven in tabel A.3.
Zowel EEM methode als de LiftVan methode zijn toepasbaar voor opdrijfsituaties als voor situaties zonder opdrijven. En in de praktijk werden (en worden soms nog steeds) opdrijfsituaties ook wel doorgerekend met de Bishopmethode, waarin schuifsterktes van de binnendijkse deklaag in het opdrijfgebied gelijk nul worden gesteld. Het onderscheid naar rekenmethode, dat vroeger werd gehanteerd om de rekenmodelonzekerheidsfactoren voor situaties met en zonder opdrijven te etiket- teren, is daarom verwarrend.
In de praktijk heeft dit wel geleid tot incorrecte interpretaties. Zo is het voorgekomen dat bij LiftVan analyses voor opdrijfsituaties, waarbij voor de twee afzonderlijke afschuifcirkels eenzelfde radius en middelpunt werd gevonden, aangenomen werd dat om die reden de (kleinere) rekenmodelonzekerheidsfactor voor de Bishop methode mocht worden toegepast.
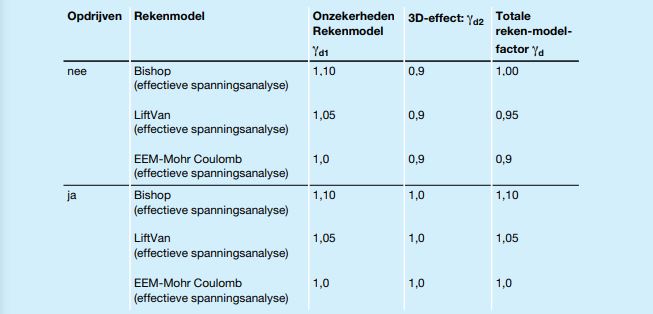
Tabel A.3 Geadviseerde aan te houden rekenmodelonzekerheidsfactoren (bron: Koelewijn et. al [29] )
