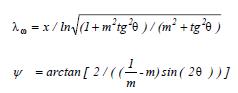Methode met gebruikmaking van de cyclische lekfactor m.b.v. een 13-uurs meting (bij par. 2.3.6)
Voor de bepaling van niet-stationaire situatie (getijde fluctuaties) bij getijde rivieren kan gebruik worden gemaakt van de methode van de zogeheten cyclische lekfactor λω (model 3B). Het subscript slaat op de cycliciteit (de frequentie is f=ω/2π). De cyclische lekfactor is significant kleiner dan de stationaire lekfactor λ, vanwege de demping en vertraging die in het cyclische gedrag doorwerken. Het in rekening brengen van cyclisch gedrag (tijdsduur hoogwater, getijden) levert een uitgekiend ontwerp.
De bepaling van de cyclische lekfactor uit dagelijkse omstandigheden is gebaseerd op peilbuiswaarnemingen gedurende een half etmaal plus een uur (13-uurs meting). Een voorbeeld van dergelijke metingen is gegeven in figuur b3.8, waarin een peilbuismeting is uitgezet tegen de getijdevariatie van de buitenwaterstand. De relatie tussen twee cyclische stijghoogtevariaties lijkt sterk op een ellips.
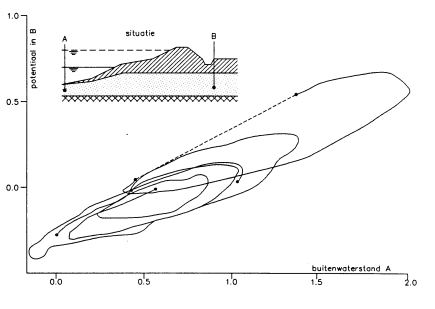
Figuur b3.8 Getijde respons in een peilbuis gedurende een aantal etmalen.
Een tijdsafhankelijke relatie tussen de twee peilbuiswaarnemingen kan worden weergegeven met de formule:
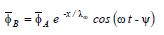 (3.2)
(3.2)
Hierin zijn ϕA en ϕB stijghoogteamplituden, is exp[-x/λω] de amplitude demping en Ψ de faseverschuiving (het faseverschil tussen het maximum in peilbuis B en in peilbuis A). Er is in theorie een eenduidig verband tussen een ellips (zie figuur 3.9) en formule (3.2), namelijk:
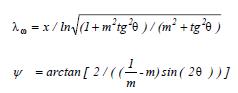
Voor de betekenis van de parameters m en wordt verwezen naar figuur b3.9.
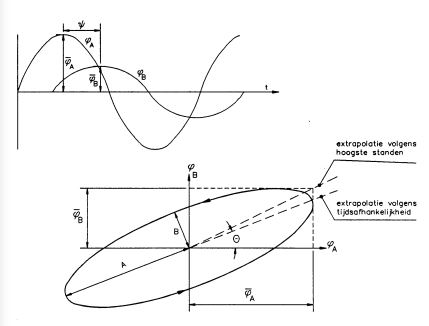
Figuur b3.9 Theoretisch verband cyclische peilbuiswaarnemingen
Hier is m = B/A: de slankheid van de ellips. Als de ellips erg smal is, geldt m « 1. In dat geval gaan bovenstaande relaties over in:
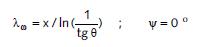 (3.4)
(3.4)
Aangezien tg θg elijk is aan φB/φA , komt deze formule overeen met de eerdere uitdrukkingen van λω (vergelijking 3.1). Door gebruik te maken van de vorm en stand van de theoretische ellips, zijn betere schattingen voor λω en Ψ te geven. Immers, de tijdsafhankelijke extrapolatie is uitgekiender dan die volgens hoogste standen (zie figuur b3.9). De werkelijke vorm wijkt meestal af van een ellips samenhangend met niet-lineaire effecten (zie figuur b3.8).
Gebleken is dat er steeds verder van de rivier meer amplitudedemping en vertraging (faseverschuiving) optreedt. De amplitudedemping is bruikbaar voor het bepalen van de lekfactor, de faseverschuiving niet.
Als een stormopzet of een hoogwatergolf een cyclisch gedrag vertoont, bijvoorbeeld een halve sinus, kan ook van de methode van de cyclische lekfactor gebruik worden gemaakt door de belasting als een voortgaande sinus te beschouwen. Dezelfde formules zijn dan bij benadering bruikbaar in het “realistische” deel van de belasting. Ook superpositie van verschillende cyclische componenten (ieder met een specifieke frequentie) is mogelijk, maar er dient dan een schaalregel in de tijd te worden toegepast (zie b3.6, figuur b3.19). De maatgevende situatie kan vervolgens worden vastgesteld door, uitgaande van de ontwerpwaterstand en de duur ervan, met de berekende -waarde uit formule 3.3 de corresponderende stijghoogte te berekenen.
Voor het Hollandprofiel geldt voor de absolute waarde bij een specifieke frequentie (de faseverschuiving is niet aangegeven):
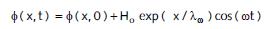
Hierin is ϕ(x,0) de gemiddelde (semi-)stationaire potentiaal in de ontwerpsituatie (startwaarde) en H0de amplitude van de fluctuaties van de ontwerpbuitenwaterstand. De stationaire potentiaal kan met de eerder beschreven methode worden vastgesteld.