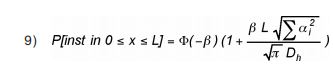Lengte-effecten - Methode ‘Probabilistische Stabiliteitsanalyse’

Lengte-effecten

In de hierboven geschetste opzet heeft de probabilistische stabiliteitsanalyse betrekking op een dwarsprofiel van de dijk. De berekende kans op afschuiven is, ruwweg gesteld, de kans dat bij het beschouwde (maatgevende) glijvlak een sta- biliteitfactor hoort die kleiner dan 1 is, of althans kleiner dan een bepaalde drem- pelwaarde q wanneer er sprake is van systematische rekenmodelonzekerheid (zie Bijlage B). Die kans is representatief voor het dwarsprofiel, of beter gezegd, een betrekkelijk korte strekking in lengterichting van de waterkering waarbinnen de ondergrondopbouw, grondeigenschappen, het waterspanningspatroon en externe belastingen weinig variëren.

In een lange strekking van de waterkering kunnen de ondergrondopbouw en de gemiddelden van de grondeigenschappen op een locatie in lengterichting variëren. Om dit in te zien kijken we naar het ruimtelijke variatiepatroon zoals geschetst in Figuur 12.

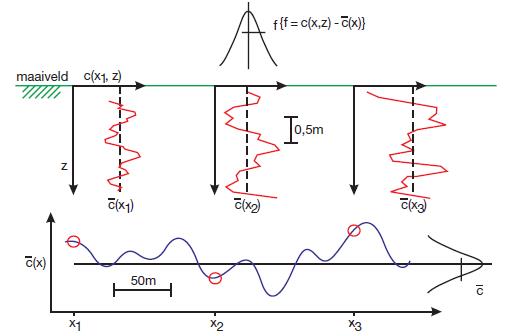
Figuur 12

Mogelijk variatiepatroon van parameter cu

De totale lengte op de x-as kunnen we opgedeeld denken in strekkingen van pakweg 50 m. Binnen elk van die strekkingen is de gemiddelde schuifsterkte ongeveer constant, maar tussen de strekkingen onderling kan die wel verschillen. In statistisch jargon: de gemiddelde schuifsterktes in de verschillende strekkingen zijn onafhankelijke realisaties. Dat impliceert dat ook de bijbehorende instabiliteit- kansen voor de verschillende strekkingen, hoewel op zich allemaal gelijk, althans voor een deel onafhankelijk zijn.

We kunnen dit vergelijken met een ketting, die op een bepaalde trekkracht belast wordt. Elk van de schakels heeft een bepaalde kans om te breken en die kans is voor elk van de schakels gelijk. De kans dat de ketting breekt, dat wil zeggen dat tenminste één schakel breekt, is ruwweg gelijk aan de kans op breuk van één schakel keer het aantal schakels. Dit wordt serie-effect genoemd.

Analoog is bij waterkeringen (en andere langgerekte aarden constructies met een talud) de kans op het optreden van instabiliteit ongeveer evenredig met de lengte van de waterkering. Dit wordt lengte-effect genoemd. Het lengte-effect kan bij benadering als volgt berekend worden aan de hand van de uitkomsten van een probabilistische analyse voor een doorsnede:

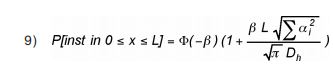
Hierin is β de betrouwbaarheidsindex, Dh de horizontale correlatieparameter (zie Bijlage B en Bijlage D), L de lengte van de beschouwde strekking, x een wille- keurige locatie binnen de strekking en zijn de αide invloedscoëfficiënten van de schuifsterkteparameters in de betrouwbaarheidsanalyse voor de dijkdoorsnede. P[inst in 0 < x < L ] is de kans dat ergens binnen de strekking met lengte L een instabiliteit optreedt. Vergelijking (9) is een verdere uitwerking van de afleiding van het lengte-effect die in het rapport ‘PROSTAB, een computerprogramma voor probabilistische analyse van stabiliteit van taluds’ [7] gegeven is.

Ten aanzien van de keuze van de lengte L in vergelijking (9) dient het volgende te worden opgemerkt. Een voor de hand liggende keuze is de fysieke lengte van de dijkstrekking die wordt beschouwd en waarvoor de invoer in de probabilistische stabiliteitsanalyse representatief is. Voor wat betreft de opbouw van de onder-grond is dat laatste vaak niet het geval. Wanneer voor het bepalen van de onder-grondopbouw een geotechnisch profiel beschikbaar is, zal voor de ‘doorsnede-analyse’ de voor de faalkans maatgevende locatie binnen de beschouwde strekking worden gekozen. Bij twijfel wordt een beperkt aantal keuzes gemaakt, waaruit de voor de instabiliteitkans maatgevende doorsnede kan blijken of waar-mee de delen van de strekking die significant bijdragen aan de instabiliteitkans kunnen worden geïdentificeerd. Voor de berekening van het lengte-effect wordt dan de lengte van het deel van de strekking waarvoor de maatgevende ondergrondo-pbouw representatief is gekozen. Ingeval er meerdere delen van de strekking significant bijdragen, worden voor die delen afzonderlijk de bijbehorende represen-tatieve lengtes bepaald en worden de bijdragen aan de instabiliteitkans van de strekking gesommeerd. Hierbij kan in beginsel rekening gehouden worden met onderlinge afhankelijkheden tussen die delen.

Opmerking: Bij het kiezen van de ‘schadefactor’ bij stabiliteitscontroles volgens de ‘Leidraad voor het ontwerpen van rivierdijken, deel 2 - benedenrivierengebied’ [4] of het ‘Technisch Rapport Waterkerende Grondconstructies’ [29] wordt, ter verdiscontering van het lengte-effect, wél de fysieke lengte van een dijkring of dijkstrekking gebruikt. Dit lijkt in tegenspraak met het bovenstaande, maar is het niet omdat in de verdiscontering van het lengte-effect in die Leidraad en dat Technisch Rapport ermee rekening gehouden is dat slechts een deel van de fysieke lengte significant bijdraagt aan het lengte-effect.