Indicatie ‘random’ onzekerheid over waterspanningsrespons
In deze paragraaf wordt nader ingegaan op de vraag wat veilige schattingen kunnen zijn voor onzekerheden met een ‘random effect’, dat wil zeggen grootheden die in de historische belastingsituatie waarschijnlijk anders gerealiseerd zouden zijn dan in een toekomstige situatie. Als voorbeeld wordt ingegaan op de grootte van niet systematisch doorwerkende onzekerheid van de waterspanningsrespons. Het gaat dus om onzekerheid van de waterspanningen die veroorzaakt wordt door niet in de modellering meegenomen zaken als initieel vochtgehalte in de dijk, bij het begin van de hoogwaterstand, veroorzaakt door neerslag in de periode voorafgaand aan die waterstand. Het effect daarvan is dat bij elke hoogwaterstand de daardoor veroorzaakte component in de waterspanningen onafhankelijk wordt gerealiseerd. Het is dus denkbaar dat daardoor bij de historische hoogwaterstand relatief lage waterspanningen zijn gerealiseerd, terwijl we er voor de toetssituatie van uit moeten gaan dat juist relatief hoge waterspanningen worden gerealiseerd. Omdat de uit- komsten van stabiliteitsanalyses, en dus ook de faalkansen, sterk afhankelijk zijn van waterspanningen, heeft deze random wisselende component in de water- spanningsrealisaties een grote invloed op de bewezen sterkte, zie ook [25].
Indicaties van de grootte van deze niet systematische waterspanningsvariaties kunnen in beginsel verkregen worden met behulp van waterspanningsmetingen bij een serie hoogwatersituaties. Als werkhypothese beperken we ons even tot meting van waterspanningen in de dijk (nabij het binnentalud). Het kan echter ook gaan om waterspanningen in grondlagen onder de dijk. In grafieken kunnen geobser- veerde waterspanningen worden uitgezet tegen de hoogwaterstand (eventueel ook als functie van de duur van de hoogwaterstand). In Figuur B 5 is de opzet
van zo’n grafiek geschetst.
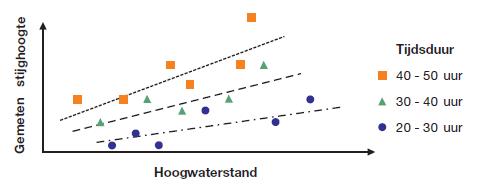
Figuur B 5
Gemeten stijghoogten versus Hoogwaterstand en Hoogwaterduur (fictief)
In deze grafiek kan op basis van de grootte van de afwijkingen tussen de werkelijk gemeten waterspanningen ten opzichte van een ‘gemiddelde’ regressielijn de standaardafwijking van de ‘toevallige’ variaties worden geschat.
In de praktijk zullen we vermoedelijk nog niet beschikken over (voldoende) metingen om tot een redelijk onderbouwde uitspraak te komen. Voor een verdere onderbouwing van het ‘Bewezen-Sterkte’-concept is het overigens wel van belang dat zulke metingen worden uitgevoerd.
Bij gebrek aan beter zullen we ons nu moeten behelpen met tentatieve schattingen van die variaties. We gaan er van uit dat we bij niet systematische onzekerheden over de waterspanningsrespons toch primair moeten denken aan effecten van
neerslag in de periode voorafgaand aan de hoogwaterstand. Deze effecten zijn in het verleden bestudeerd [6]. Doel van die studie was het vaststellen van ontwerp-waarden voor de verhoging van waterspanningen als gevolg van extreme neerslag, ten behoeve van stabiliteitscontrole. In dat kader zijn berekeningen gemaakt van stijghoogtetoenames ter plaatse van de binnenkruinlijn voor een aantal locaties langs de Lekdijk bij Nieuw Lekkerland en Streefkerk (Alblasserwaard). Figuur B 6 is ontleend aan bovengenoemd rapport. De stijghoogtetoenames zijn berekend met behulp van het programma SWANFLOW, daarbij is rekening gehouden met percolatie van neerslag in gedeeltelijk verzadigde grond binnen het dijklichaam en afstroming van neerslag langs het binnentalud. De berekeningen zijn geverifieerd met behulp van metingen van freatische stijghoogten in de dijk beneden de binnen-kruinlijn. In Figuur B 6 (ontleend aan [6]) zijn de gemeten stijghoogten (ten opzichte van een nulsituatie, dat wil zeggen gemeten freatische stijghoogten gedurende een lange droge periode) horizontaal uitgezet tegen (verticaal) de cumulatieve neerslag gedurende 7 dagen voorafgaande aan de meting. De getrokken lijnen reflecteren de extrapolatie met behulp van SWANFLOW-berekeningen naar extreme neerslagsituaties, maar die zijn voor de analyse hier niet van belang. Van belang zijn de meetresultaten die stijghoogtetoenames reflecteren als gevolg van niet extreme neerslag.
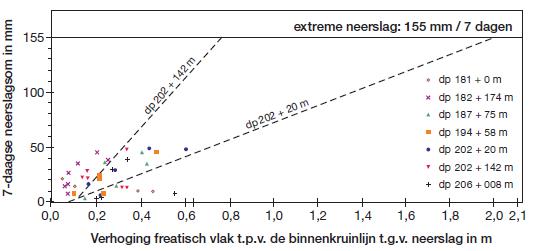
Figuur B 6
Gemeten freatische stijghoogtetoenames (hor.) versus cumulatieve neerslag (vert.).` Figuur ontleend aan [6]
Enig gevoel voor de frequentie waarmee (7-daagse) cumulatieve neerslagen, in de orde zoals die zijn voorgekomen bij de metingen in Figuur B 6, kunnen we krijgen we door terugrekening van de analyse van Swart. Hij komt aan de hand van door het KNMI verstrekte gegevens over relaties van combinaties neerslagintensiteit en neerslagduur en jaarkans van voorkomen op een cumulatieve (7-daagse) neerslag van 155 mm die met een jaarkans van 1/4000 wordt overschreden. Wanneer we een eenvoudige extreme waarde kansverdeling veronderstellen, namelijk een exponentiële verdeling, dan kunnen we uitgaande van dit resultaat de (indicatieve) jaarkansen voor lagere cumulatieve neerslagen berekenen. We vinden dat cumula- tieve 7-daagse neerslag van 50 mm, respectievelijk 25 mm en 10 mm met kansen van 0,05, respectievelijk 0,20 en 0,55 per jaar worden overschreden. Dit betekent dat we de cumulatieve gemeten neerslagen, en bijbehorende freatische stijghoogte- toenames van enkele decimeters ten opzichte van droge periodes, zoals die voor- komen in Figuur B 6 vooralsnog niet kunnen uitsluiten bij extreme hoogwatersitua- ties. We zien ook een behoorlijke spreiding in de realisaties van stijghoogtetoename bij de verschillende neerslagsituaties.
Al met al bevestigt dit beeld dat bij de vergelijking tussen een (of meer) overleefde hoogwatersituatie(s) en de toetssituatie een niet voorspelbare (want niet systema-tische) component in de waterspanningsrespons een rol speelt. In eerdere proba-bilistische ‘Bewezen-Sterkte’-analyses [26] is aangetoond dat dit een aanzienlijk effect heeft op de resultaten van een ‘Bewezen-Sterkte’-analyse. Daarbij is uitge-gaan van verschillende standaardafwijkingen van de niet systematische component van de waterspanningsvariaties. Aan de hand van de hierboven gegeven beschou-wing wordt geconcludeerd dat een standaarddeviatie σwvan 0,15 m realistisch is.
In de deterministische ‘Bewezen-Sterkte’-analyse (correctiefactoraanpak) zoals beschreven in het Technisch Rapport, kan er op grond hiervan in beginsel van worden uitgegaan dat variaties van de freatische lijn ter plaatse van de binnenkruin- lijn als gevolg van normale (niet extreme) neerslagvariaties ± 0,25 m (ten opzichte van gemiddeld) kunnen bedragen. Deze grenzen zijn te beschouwen karakteristieke waarden van het neerslageffect (1,64 · σw≈ 0,25m). Een en ander impliceert dat voor de freatische waterspanningen in de historische situatie uitgegaan zou moeten worden van een freatische stijghoogte ter plaatse van de binnenkruinlijn die circa 0,5 m lager ligt dan aangenomen wordt voor de toetssituatie. Indien gegevens over de neerslaghoeveelheden in de historische situatie achterhaald kunnen worden, en vervolgens hieruit blijkt dat er destijds sprake is geweest van een aanzienlijke hoeveelheid neerslag, dan kan van een hogere ligging van de freatische lijn in de historische situatie worden uitgegaan, hetgeen uiteraard gunstig is voor het bewijs.

