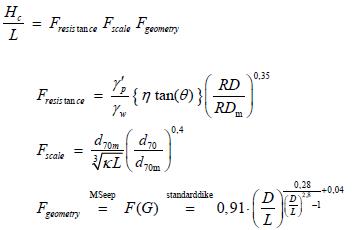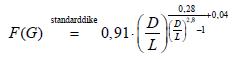Het aangepaste rekenmodel van Sellmeijer vervolg - Rekenmodellen en rekenregels

Hierbij dient te worden opgemerkt dat de in Figuur 5.4 door Silvis beschreven gradiënten niet in de IJkdijkexperimenten zijn teruggevonden.

In een vervolgonderzoek [Sellmeijer et. al.,1989] is een soortgelijke rekenexercitie uitgevoerd voor de ondergrondconfiguratie die in Figuur 5.5 is weergegeven.

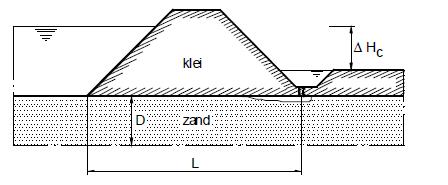
Figuur 5.5 Basisconfiguratie rekenmodel Sellmeijer [Sellmeijer et al., 1989]

In het kader van het project SBW Piping is fundamenteel onderzoek verricht naar het mechanisme piping. Het uitgevoerde onderzoek omvatte proeven op kleine (0,35 m), medium (1,35 m) en grote schaal (15 m). Het doel van het onderzoek was een hervalidatie van de theorie van Sellmeijer zoals beschreven in het voormalige TR Zandmeevoerende Wellen [TAW, 1999]. Het model en de voor de toetsing te gebruiken rekenregel zijn opnieuw gekalibreerd met de nieuwe experimentele data.

De eigenschappen uniformiteit, hoekigheid, doorlatendheid en korrelgrote kunnen en hoeven in proeven voor Nederlandse omstandigheden niet onafhankelijk te worden gevarieerd omdat de uniformiteit zoals de meeste korrelgroottekarakteristieken direct gekoppeld is aan de doorlatendheid.

De invloed van zandparameters is door middel van een multivariate analyse op de resultaten van kleine- en medium-schaalexperimenten onderzocht en gekwantificeerd. De multivariate analyse geeft een empirische relatie tussen de verschillende zandeigenschappen en het verval dat leidt tot een doorgaande pipe. Mede op basis van de resultaten van deze multivariate analyse is een aangepaste rekenregel voor piping afgeleid [Knoeff, Sellmeijer, Lopez & Luijendijk, 2009].

De oorspronkelijke regel van Sellmeijer is gebaseerd op een stromingsberekening en een uitwerking van het krachtenevenwicht. In deze regel is, zo ver mogelijk bij de toenmalige stand van de kennis, de fysica van het pipingproces meegenomen. In de aangepaste rekenregel is dat gedeeltelijk nog het geval, zo komt het zogenaamde kwelweglengte- schaaleffect dat is gevonden in proeven op medium en grote schaal overeen met de beschrijving in de regel van Sellmeijer. Voor het kwelweglengte-schaaleffect hebben de proeven de regel van Sellmeijer dus bevestigd. Voor andere parameters is dit niet het geval en moet op basis van de multivariate analyse worden geconcludeerd dat de metingen een ander verband aantonen dan in de oorspronkelijke regel van Sellmeijer wordt voorgesteld. Waarschijnlijk is de fysische beschrijving in de regel van Sellmeijer voor deze parameter onvolledig. Op dit moment is er nog geen betere fysische beschrijving voorhanden en is het verband tussen die parameters en het kritieke verval alleen empirisch vastgesteld op basis van proeven en de multivariate analyses. De zo gevonden verbanden zijn alleen geldig in de range waarbinnen de proeven zijn uitgevoerd.

De regel is afgeleid en gevalideerd voor Nederlandse zanden met een korreldiameter d70tussen de 150 en 500 µm, waarbij de relatieve dichtheden groter zijn dan 50% en de uniformiteit varieert tussen 1,5 en 2,5. In deze aangepaste rekenregel, welke gebaseerd is op

het twee-krachtenmodel, is de relatieve dichtheid als extra parameter toegevoegd en is de invloed van de d70verminderd. De invloed van de korreldiameter op het kritieke verval is in de rekenregel gereduceerd in de schalingsfactor Fscale. Ofschoon de fysica ervan nog niet goed begrepen is, is dit volgens de uitgevoerde metingen de juiste plaats.

Op basis van het twee-krachtenmodel van Sellmeijer is voor een standaard dijkconfiguratie met een homogene zandlaag onder een ondoorlatende laag de volgende rekenregel geformuleerd. Deze rekenregel kan worden geordend in clusters.

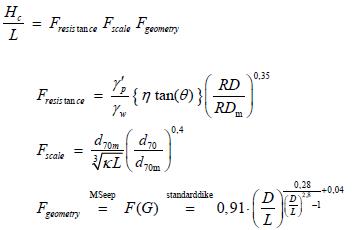
(5.8)

waarin:

Hc kritieke verval over de waterkering [m]

’p (schijnbaar) volumegewicht van de zandkorrels onder water [kN/m3]

 w volumegewicht van water [kN/m3]

θ rolweerstandshoek van de zandkorrels [˚]

η coëfficiënt van White [-]

 intrinsieke doorlatendheid van de pipinggevoelige/bovenste zandlaag [m²] d70 70-percentielwaarde van de korrelverdeling [m]

d70m gemiddelde d70 in de kleine schaalproeven (2,08 E-4m) D dikte van de zandlaag [m]

L lengte van de kwelweg (horizontaal gemeten) [m] RD relatieve dichtheid [-]

RDm gemiddelde relatieve dichtheid in de kleine schaalproeven (0,725)

Er kunnen drie factoren worden onderscheiden: een resistance, een scale en een geometry factor.

De eerste factor beschrijft het grensevenwicht van zandkorrels op de bodem van de pipe. De tweede term reflecteert de verhouding tussen de processchaal van het mechanisme dat voor korreltransport zorgt en de processchaal van de grondwaterstroming die dit transportmechanisme aandrijft. Voor schaalproeven is dit een belangrijke verhouding. De laatste term beschrijft de invloed van de vorm van de geometrie van de ondergrond op de grondwaterstroming. Deze is afhankelijk van de verhouding tussen dikte en lengte van de aanwezige zandlagen. In geval van een meerlagensysteem is deze factor ook afhankelijk van het doorlatendheidscontrast tussen de zandlagen. De geometry factor is situatieafhankelijk en moet worden bepaald met het grondwaterstromingsmodel MSeep. Voor een standaard

66 van 345

dijkconfiguratie met een homogene zandlaag onder het ondoorlatende dijklichaam wordt de factor benaderd door:

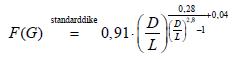
(5.9)

De intrinsieke doorlatendheid  [m2] kan worden afgeleid uit schattingen van karakteristieke waarde van de specifieke doorlatendheid [m/s] van de pipinggevoelige bovenste zandlaag.

De relatie is:

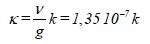
(5.10)

Waarin  de kinematische viscositeit is (≈ 1,33*10-6m2/s voor grondwater van 10° Celsius) en g de versnelling van de zwaartekracht (9,81 m/s2). De doorlatendheid kan op verschillende manieren worden geschat of gemeten. In [TAW, 1994] is een procedure aangegeven om de doorlatendheid te berekenen aan de hand van zeefanalyses van het zand in de zandlaag (zie

ook Bijlage 2). Denkbaar is ook dat schattingen van de doorlatendheid worden verkregen aan de hand van in situ proeven (pompproef, fallinghead-proeven, monopoolmetingen, etc.) of uit REGIS II bestanden4 over diepere boringen. Het verkrijgen van een betrouwbare schatting

van de doorlatendheid is overigens een moeilijk probleem, waarbij de effecten van heterogeniteit van de zandlaag een lastige rol spelen. In de piping-formule moet met een conservatieve schatting (hoge representatieve waarde) van de doorlatendheid worden gerekend.