Bijzondere aspecten - Processen en modellen

Bijzondere aspecten

De capillaire zone boven de freatische lijn

Bij de beoordeling van dijkstabiliteit wordt aanbevolen geen gebruik te maken van het sterkte-effect als gevolg van onderdruk in de capillaire zone.

Het stroombeeld in de dijk wordt aan de bovenzijde in feite niet echt begrensd door de freatische lijn. De freatische lijn is in wezen de hypothetische positie waar de waterdruk gelijk is aan de atmosferische druk. Boven die lijn is, afhankelijk van de grondsoort, een zekere zone aanwezig waarin zich door capillaire opstijging ook grondwater bevindt: de capillaire zone. Daar stroomt het water ook, maar verticaal. De grond direct boven de freatisch lijn is in het algemeen volledig met water verzadigd, terwijl verder naar boven de verzadigingsgraad afneemt. Een duidelijke begrenzing van de volledig verzadigde zone boven de freatisch lijn is niet aan te wijzen. In de praktijk legt men deze grens wel bij een verzadigingsgraad van 75%. De capillaire opstijging is afhankelijk van de grondsoort en bedraagt gemiddeld:

• in grof zand:                                           ca. 0,02-0,05 m;

• in matig fijn tot matig grof zand:       ca. 0,12-0,35 m;

• in silt:                                                       ca. 0,70-1,50 m;

• 
  

  in klei:                                                      ca. 2-4 m of meer.

  

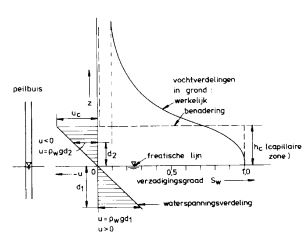
  Symbolen

  u     = waterspanning:

  uc   = capillaire waterspanning

  Ρw  = volumieke massa water

  g     = versnelling zwaartekracht

  d     = hoogte ten opzichte van de freatische lijn

  Figuur 2.3 Capillaire zone

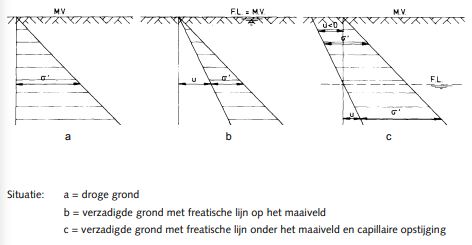
  Er is in de capillaire zone een bijzonder mechanisch effect op de korrelspanning. Door de negatieve waterspanningen, dat wil zeggen een onderdruk ten opzichte van de atmosferische druk, nemen de korrelspanningen in de capillaire zone toe (figuur 2.3). Dit aspect kan een belangrijke rol spelen bij de draagkracht van de grond, met name ten aanzien van de stabiliteit van taluds en de begaanbaarheid van binnendijkse bermen en de kruin van de dijk.

  Vergroting van de schuifweerstand van de grond is te bewerkstelligen door de freatische lijn in de dijk middels een drainageconstructie laag te houden. Hierdoor stijgt de capillaire korrelspanning in de grond, mits de doorlatendheid van de grond dit toelaat.

  Wat betreft de begaanbaarheid, bepaald door de korrelspanningen ’ direct onder het maaiveld, spreekt figuur 2.4

  voor zich. De grootste draagkracht van het maaiveld is aanwezig in het geval van capillaire opstijging.

  Een belangrijk aspect dient hierbij in overweging te worden genomen. Als de capillaire zone groot is (met een hoge verzadigingsgraad) dan is er maar weinig filtratiewater nodig om de freatische lijn te laten stijgen. Het sterkte effect door onderdrukken is dan snel weg. In zand is dit verschijnsel zelf te constateren op het strand, vlakbij de waterlijn. Net buiten de waterlijn is het natte zand bijzonder stevig, net in het water slap.

Figuur 2.4 Korrelspanningen en waterspanningen direct onder het maaiveld

De freatische opbolling bij infiltratie

Nederland is in bepaalde seizoenen regenachtig. De neerslag draagt voor een deel (ca. 20%) als infiltratie bij tot het grondwater. De grondwaterspiegel stijgt en dit leidt mettertijd tot zijdelingse afstroming naar de rand (sloten, dijkhellingen). Er treedt opbolling op van de freatische lijn. De hiermee samenhangende verhoging van de waterspanningen heeft invloed op de mechanische stabiliteit van een dijk.

Veel dijken zijn in de loop van eeuwen ontstaan, en deze oudere dijken zijn steeds opgehoogd met verschillende materialen. Het verkeer erop zorgde voor compactie. Oude dijkkernen zijn derhalve relatief dicht en ondoorlatend. De opbolling van de freatische lijn in deze dijken komt langzaam tot stand maar is ook hardnekkig. Het is niet ongebruikelijk dat in dijken een relatief (soms erg) hoge freatische lijn wordt gevonden. Bovendien is er in deze dijken veelal een relatief grote capillaire zone. Een verzadigde dijk is meer kwetsbaar, zowel voor macrostabiliteit als voor erosie.

Indringingslengte

De hoogte waarover de waterspanningsvariaties in het watervoerend pakket van betekenis zijn voor de waterspanningen in het samendrukbare pakket, wordt aangeduid met indringingslengte L. Deze geeft de zone aan waarin de toegenomen waterspanning merkbaar is. De indringingslengte speelt een rol bij freatische stijging in een zanddijk en bij consolidatie op het grensvlak zandlaag-toplaag.

De mate van indringing van een hogere stijghoogte vanuit een watervoerende zandlaag naar een relatief slecht doorlatende afdekkende klei- of veenlaag is van belang voor de binnenwaartse macrostabiliteit van een waterkering. Door hogere waterspanningen nemen de korrelspanningen en maximaal opneembare schuifkrachten van de grond af en kan een instabiliteit optreden.

In figuur 2.5 staat schematisch aangegeven wat wordt verstaan onder de indringingslengte. Voor de stabiliteitsberekeningen wordt in deze zone waarover de indringingslengte zich uitstrekt, een lineaire benadering van het waterspanningsverloop aangenomen. Buiten de zone worden de waterspanningen geacht niet beïnvloed te zijn. De indringingslengte hangt samen met de doorlatendheid (de af- of instroomcapaciteit) en de freatische of elastische berging. De indringingslengte is derhalve tijdsafhankelijk. Naarmate de hoogwaterbelasting langer duurt, neemt de indringingslengte proportioneel met de wortel van de tijd toe:

L (:) √t.

Als de belastingduur zo lang is dat L groter wordt dan de dikte van het samendrukbare pakket, dan is de grondwaterstroming feitelijk stationair geworden. Aangezien dit bijvoorbeeld voor benedenrivierdijken zeker niet het geval is, wordt de indringingslengte in de stabiliteitsanalyse gebruikt om de tijdafhankelijke grondwaterstroming quasi-stationair te modelleren. Daarbij dient rekening te worden gehouden met het lokale proces: samendrukking (A) en zwel (B).

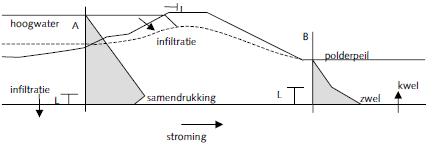
Figuur 2.5 Indringing waterspanningen en relevante processen

De grootte van de indringingslengte hangt af van de geohydrologische parameters en het verloop van de waterstand.

De wijze waarop de indringingslengte kan worden berekend is gegeven in bijlage b4.3.

Lekfactor

De grondwaterstroming onder de dijk hangt samen met de doorlaatcapaciteit van het systeem. In het Hollandprofiel wordt die capaciteit bepaald door de weerstand van de toplaag en het doorlaatvermogen van de onderliggende zandlaag. Beide fenomenen tezamen worden uitgedrukt in de zogeheten lekfactor , een lengtemaat voor de watervoerende zandlaag en in die zin vergelijkbaar met de indringingslengte in de samendrukbare toplaag. De lekfactor is gelijk aan de wortel van het product van doorlaatvermogen of transmissiviteit T (kD-waarde) en toplaagweerstand c (hydraulische weerstand):

λ= √(Tc)

waarin:

λ   = lekfactor [m]

T   = transmissiviteit (kD-waarde) van het zandpakket [m2/dag]

c   = toplaagweerstand/hydraulische weerstand [dag] k = doorlatendheid van zandlaag [m/dag]

D  = dikte van de zandlaag [m]