De stijghoogte in de zandlaag geven we aan met Φ z(x). Deze is een functie van de horizontale plaatscoördinaat x (-Lv≤ x ≤ 0), waarbij Lvde lengte van het voorland is. In eerste instantie gaan we uit van stationaire stromingen. Het verhang over de kleilaag op een bepaalde plaats –x is - (Φ –z(x) - H) / dI, waarin H de buitenwaterstand is en dIde dikte van de afdekkende laag in het voorland. De lek door het voorland is kI* (Φ –z(x) - H) / dI, waarin kIde doorlatendheid is van de afdekkende laag. Behoud van massa leidt tot de volgende differentiaalvergelijking voor de stijghoogte Φ zin de zandlaag, in een stationaire toestand:
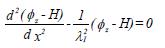 A(1.1)
A(1.1)
waarbij -Lv ≤ x ≤ 0 is en λI de spreidingslengte voor het voorland:
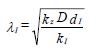 A(1.2)
A(1.2)
waarin kI en dI respectievelijk de (verticale) doorlatendheid [m/s] en dikte van de afdekkende laag in het voorland zijn.
Analoog wordt voor gebied III de stijghoogte beschreven door:
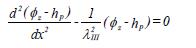 A(1.3)
A(1.3)
waarbij L2≤ x < ∞ is, hphet polderpeil (of het maaiveldpeil indien geen vrije waterspiegel aanwezig is) en λIIIde spreidingslengte van het achterland:
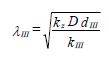 A(1.4)
A(1.4)
Hierin zijn kIII en dIII respectievelijk de (verticale) doorlatendheid [m/s] en dikte van de afdekkende laag in het achterland.
Voor het gebied 0 ≤ x ≤ L2zou ook een vergelijking moeten worden opgesteld, analoog aan A(1.1) en A(1.3). De stroming door het dijklichaam is echter niet verticaal, waardoor het afleiden van een lekterm problematisch is. Omdat de lek naar het dijklichaam toe naar verwachting klein ten opzichte van de lek door de voorland- en achterlandlaag wordt die verwaarloosd. De vergelijking voor de stijghoogte in de zandlaag in gebied II wordt dan:
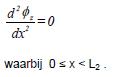
Randvoorwaarden voor het probleem zijn: Φz(-Lv) = H en Φz(∞) = hp, terwijl op de overgangen x=0 en x=L2in het zand continuïteit van stijghoogte en horizontaal stromend debiet geldt.
Daarmee luidt de oplossing (bij gelijke kD waarden van de zandlaag in de drie gebieden):
- in gebied I (-Lv ≤ x ≤ 0):
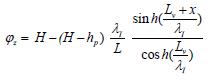 A(1.6)
A(1.6)
- in gebied II (0 ≤ x ≤ L2):
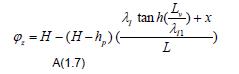 A(1.7)
A(1.7)
- en in gebied III (L2 ≤ x ≤ ∞):
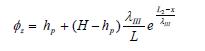 A(1.8)
A(1.8)
Hierin is:
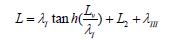 A(1.9)
A(1.9)
In bovenstaande vergelijkingen zijn sinh(), cosh(), en tanh() respectievelijk de hyperbolische sinus-, cosinus en tangentfuncties.
In het WATEX rekenmodel wordt gebied II verwaarloosd (L2= 0), terwijl het gebied III kan worden opgesplitst in een gebied direct achter de dijk en een gebied ver weg van de dijk (het zogenaamde Drie-sectie model).
De eerste term in A(1.9) geeft de effectieve lengte van het voorland aan; voor x < - λI tanh(Lv/ λI) is de stijghoogte ongeveer gelijk aan H. In de berekening van de aanwezige kwelweglengte (paragraaf 5.6.1) wordt deze maat dan ook aangehouden om de invloed van het voorland te berekenen.
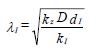 A(1.2)
A(1.2)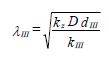 A(1.4)
A(1.4)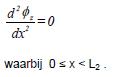
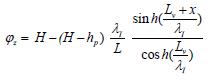 A(1.6)
A(1.6)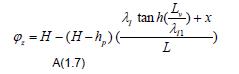 A(1.7)
A(1.7)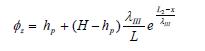 A(1.8)
A(1.8)