Kansen gedrag stormvloedkeringen - Bijlage C Probabilistisch model van het benedenrivierengebied

Kansen gedrag stormvloedkeringen

De werking van de stormvloedkeringen in de Nieuwe Waterweg en het Hartelkanaal heeft invloed op de hoge waterstanden in het benedenrivierengebied. Het moment van sluiten van de keringen wordt genomen op basis van voorspelde waterstanden. In die voorspellingen zitten onzekerheden. Daardoor is het mogelijk dat de kering, op basis van de voorspellingen, open blijft staan, terwijl de kering op basis van de werkelijk opgetreden waterstanden gesloten had moeten worden of andersom.

In het probabilistisch model is de zogenaamde sluitfunctie geïntroduceerd. De sluitfunctie geeft de waterstand in de Maasmond aan als functie van de q, r en u waarbij precies aan de sluitcriteria wordt voldaan.

Het huidige sluitcriterium van de Hartel- en Maeslantkering is: Keringen sluiten op het moment dat de voorspelde waterstanden in Rotterdam en/of Dordrecht de 3,00 m resp. 2,90 m+NAP overschrijden.

We kennen dus nu de waterstand Maasmond gegeven q, u en r waarbij de kering gesloten zal worden. Zoals eerder opgemerkt is deze waterstand niet nauwkeurig te voorspellen. Op basis van een studie door RIKZ (Kroos, 1999) is er van uitgegaan dat de voorspelfout nor- maal verdeeld is met een gemiddelde waarde van -0,09 m en een standaardafwijking van 0,18 m. (Er wordt dus systematisch 0,09 m te laag voorspeld4.) De kans dat de stormvloedkeringen open staan gegeven de rivierafvoer q, de windsnelheid u, de zeewaterstand m en de windrichting r wordt gegeven als:

p(O|q,u,m,r)

4 Inmiddels zijn er nieuwe waarden bekend op basis van een analyse voor de periode 1990-2004. De nieuwe waarden zijn μ = -0,07 en σ = 0,12 m (Kroos, 2006)

en de kans dat de stormvloedkeringen dicht staan wordt gegeven als:

p(D|q,u,m,r)

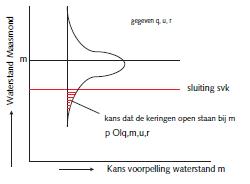
Gegeven de normaal verdeelde voorspelfout kan de kans op geopende kering bij m,q,u en r worden berekend door het gearceerde oppervlak van Figuur C.7 te integreren.

In deze figuur wordt uitgegaan van een gegeven q, u en r. De waterstand bij Rotterdam en Dordrecht hangt dan alleen af van de zeewaterstand m.

Om de werkelijk opgetreden zeewaterstand m is een kansverdeling getekend van de voor- spelde waterstand. De rode lijn geeft de zeewaterstand aan die tot sluiting van de kering leidt. Het gearceerde oppervlak geeft nu de kans aan dat de voorpelde waterstand lager is dan het sluitcriterium en dat de kering dus open blijft.

De kans op een gesloten kering is dan natuurlijk:

p(D’|q,u,m,r) = 1- p(O’|q,u,m,r)

Hier wordt resp. D’ en O’ gebruikt omdat hier alleen nog de voorspelfouten zijn meegeno- men. De voorspelfout is echter niet de enige reden dat de stormvloedkeringen ten onrechte geopend kunnen blijven.

Figuur C.7 Kans op geopende sv keringen

De stormvloedkeringen kunnen ook falen. De gangbare praktijk is om aan te nemen dat afhankelijk falen optreedt. Dat betekent dat beide keringen tegelijkertijd falen, zodat ze effectief in de berekeningen als ‘één kering’ kunnen worden beschouwd. Geerse (2003a) geeft aan dat dat een conservatieve inschatting is, maar gerechtvaardigd gezien de onzeker- heden waar men mee te maken heeft.

Voor de HR 2001 is een faalkans α van 0,001 aangenomen. Ofwel 1 maal falen (lees niet sluiten) op de duizend sluitingen. Bij de eerder gegeven kans op de ten onrechte geopende kering p(O’|q,u,m,r) dient nu nog opgeteld te worden de kans dat de kering door falen open staat. In formulevorm:

p(O|q,u,m,r) = p(O’|q,u,m,r) + α. p(D’|q,u,m,r)

Voor de kans op de ten onrechte dichte stormvloedkeringen geldt dan

p(D|q,u,m,r) = 1 - p(O|q,u,m,r)

De faalkans van de stormvloedkeringen is onderwerp van studie geweest. Voor de TMR2006 zal waarschijnlijk worden gerekend met een grotere faalkans, welke op 0.01 gesteld zal worden. Ofwel 1 maal falen (lees niet sluiten) op de honderd sluitingen.