Grondwaterpotentiaal bij niet-stationaire stroming - Bijlage

Bepaling ,·an ). en J.;'., uit peilbuiswaarnemingen

De cyclische lekfactoren kunnen worden berekend uit de grondparameters die in het laboratoriu m zijn bepaald (par. 7.3.1.2), maar ook kan de bepaling plaatsvinden uit meting van peil buizen gedurende een getijgolf.

De meting wordt meestal in 13 uu r uitgevoerd.

De bepaling geschiedt in twee stappen:

1. bepaling van de cyclische lekfactor ). voor het achterland;

2. bepaling van de cyclische lekfactor ).;'., voor het voorland.

   Voor de eerste stap kan een gemiddelde waarde voor ). worden gevonden met behulp van de methode der kleinste kwad raten:

   

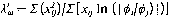
   [m] (12.14)

   hierin is:

   xij = de afstand tussen peilbuis i en j

   (lood recht op de dijkas gemeten)

   ¢;, </Jj = de desbet reffende amplitude in peilbuis i,

   respectievelijk j

   [ml [m]

   

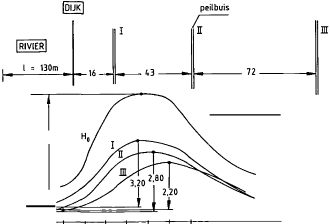
   Als voorbeeld is in figuur B 12.4 schematisch een situatie gegeven, in dit geval voor een hoogwatergolf.

   PEILBUISSYSTEEM

   4,40

   uur

   10 15 20

   PEILBUISRESPONS

   figuur B 12.4

   166

   432 + 722 + 1152

   ,l' = = 306 m

   w 3,2 2,8 3,2 '43 I n -+ 72 In -+ 115 ln -

   2,8 2,2 2,2

   J;'., word t iteratief bepaald uit form ule 12.5, hetgeen op een microcom puter eenvoudig program meerbaar is. Door de berekende dempingsterm te vergel ijken met de gemeten waarde op de locatie I, II en III kan J;'., in enkele stappen worden bepaald.

   C. Berekening potentiaal bij andere golfperioden

   De voor een getijgolf verkregen waarden mogen niet voor een stormvloed van meer­ dere getijgolven of een hoogwatergolf van meerdere dagen word en toegepast. Daarvoor dienen de waarden ofwel te worden bepaald uit meti ngen bij deze golfperioden dan wel te worden gerelateerd aan de 13-uurs-meting als volgt:

   Voor een gegeven situatie zullen ,l', ,l'' en t1, niet veranderen, zodat geldt:

   O' = A y'w is constant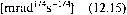

   en

   O = x;,, y'w is eveneens constant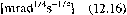

   In veel gevallen is fJ ongeveer nul (brede rivier, dun kleidek op het voorland). De formule voor de amplitude in het achterland is dan als functie van w, Q' en O :

   ¢(x, w) = Ho exp (-x y'w/0')/(1 + 0 /0') [m] (12.17)

   De ampl itude voor andere waa rden van w kan hieruit nu eenvoudig worden vastgesteld. Uitwerking van de amplitudede_mping op positie x bij frequentie w geeft uitgaande van een gemeten gedrag op positie· x111en frequentie w 111 :

   ¢(x, w) = Ho A( ¢111/fl 0111) 8[m] (12.18)

   met

   -

   A = (1 + 0 /0') 8

   1 [-] (12.19)

   en

   B = (x/ x 111 )V w/ w111 [-] (12.20)

   waarbij de suffix m staat voor de meting.

   Voor andere gevallen ( fJ f 0) kan men de amplitudedemping en faseverschu iving bij andere w berekenen door consequente substitutie van de bepaalde waarden van Q' en Q in formule 12.5.

   167

   D. Superpositie van sinusvormige golven

   Superpositie van 2 of meer sinusvormige golven is mogelijk, mits de toplaag relatief dik is en de grenspotentiaal niet wordt bereikt.

   Veelal is een willekeu rige hoogwaterbelasting in een beperkt aantal golven te verdelen, bijvoorbeeld getij, stormvloed en rivierafvoergolf.

   

   Hiervoor is een in situ meting met minstens twee peilbuizen in het achterland vol­ doende.

   

   

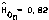
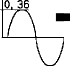
   o·

   0. o. 23

   t i j d

   figuur B 12.5

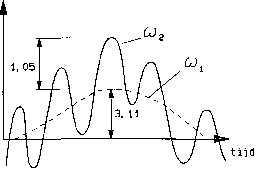
   Als voorbeeld wordt een hoogwaterbelasti ng met getij, zie figuu r 812.5, geanalyseerd met de informatie uit een 13-uurs peil buismeting.

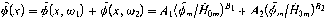   [m] (12.13)

   Voor een positie x = Xm, Wm = 0,000145 (getijde), w 1 = Wm en w2 = 0,3wm (stormvloed) volgt:

   B, = Ywif wm = 1 en

   B2 = Yw2/W m = VC),3 = 0,74

   met 0 /0' = 0,23 volgt voor A:

   -

   A , = (1 + 0,23)0= 1 en A 2= (1 + 0,23)0,74 1 = 0,948

   met <Pm/ Hom = 0,44 volgt voor de maxi male :,vaterspanning op positie x = Xm :

   ¢(x) = 1(0,44) 11,05 + 0,948(0,44) 0• 743,11 = 0,462 + 1,606 = 2,07 m