Voorbeeld probabilistische berekening van een kistdam - Bijlagen

Wandwrijvingselementen

Het bezwijkmechanisme wordt opgedeeld in 7 wandwrijvingselementen. Wandwrijvingselementen 2, 4, 6 en 7 bevinden zich in de bovenste grondlaag; wandwrijvingselementen 1, 3 en 5 bevinden zich in de onderste laag. De scheiding tussen de wandwrijvings-elementen 6 en 7 wordt gevormd door de overgang gedraineerd/ongedraineerd gedrag. De dikte van de wandwrijvingselementen is per definitie gelijk aan 1mm.

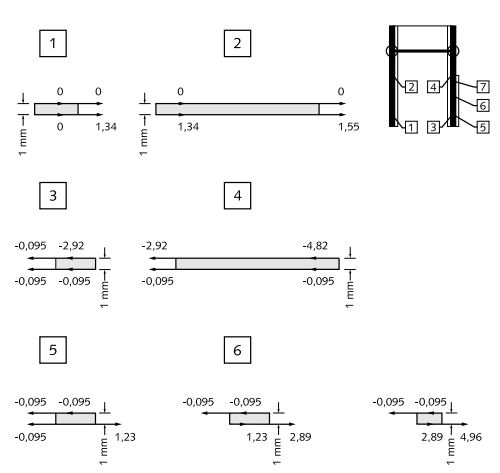
Figuur 2.4 Wandwrijvingselementen met incrementele verplaatsingen

In figuur 2.4 zijn de wandwrijvingelementen vergroot weergegeven, waarbij de elementen 90° zijn gedraaid met de klok mee. Deze werkwijze heeft tot voordeel dat in de spreadsheets alleen de incrementele verplaatsingen in langsrichting hoeven te worden opgegeven. De pijlen in de figuur geven de richting van de incrementele verplaatsingen aan; de cijfers de grootte van de incrementele verplaatsing in meters. De incrementele verplaatsingen zijn direct uit de PLAXIS uitvoer gehaald, zijnde de incrementele verplaatsing van de interface-elementen.

Schuifvoegelementen

Het bezwijkmechanisme wordt opgedeeld in 2 schuifvoegelementen. Beide schuifvoeg- elementen zijn gelegen in de onderste grondlaag. De dikte van de schuifvoegelementen is gelijk aan 0,1m.

In figuur 2.5 zijn de schuifvoegelementen vergroot weergegeven. De pijlen in de figuur geven de richting van de incrementele verplaatsingen aan; de cijfers de grootte van de incrementele verplaatsingen in meters. De incrementele verplaatsingen zijn direct uit de PLAXIS uitvoer gehaald, zijnde de incrementele verplaatsingen van de knopen ter plaatse van de hoekpunten van de schuifvoegelementen.

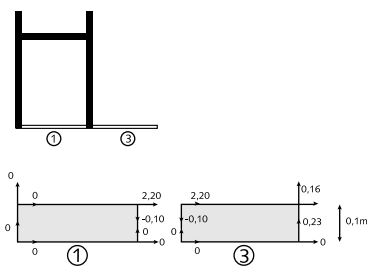
Figuur 2.5 Schuifvoegelementen met incrementele verplaatsingen

Inleiding

Opmerking

In dit hoofdstuk wordt, in tegenstelling tot de rest van het rapport, de notatie Cu gebruikt in plaats van fundr vanwege de afgedrukte voorbeelden van de spreadsheetmodellen.

In dit hoofdstuk wordt de praktische toepassing van de spreadsheets UNDRAINE, ARBEID en SOMARARBEID besproken.

In UNDRAINE wordt een probabilistische niveau 2 analyse uitgevoerd voor de ongedraineerde schuifsterkte Cu. Het resultaat is de verdelingsfunctie van Cu en de schuifsterkte Cua voor de gemiddelde sterkteparameters ca en φa. De verdelingsfuncties van Cu en de schuifsterkte Cua zijn invoer voor het spreadsheetmodel ARBEID.

In ARBEID wordt de plastische energie in een kinematisch element geïntegreerd. Deze integratie moet worden uitgevoerd voor µ(Cu), σ(Cu) en Cua. Dit resulteert in een verdelingsfunctie van de energie µ(Εe ), σ(Εe ), en een waarde Εe a voor de energie bij gemiddelde parameters. De verdelingsfunctie µ(Εe ), σ(Εe ), en de waarden Εe a zijn invoer voor het spreadsheetmodel SOMARBEID.

In SOMARBEID worden voor alle kinematische elementen en laagscheidingen waarden µ(Εe ), σ(Εe ), en Εe a ingevuld, en de gewenste waarde voor het betrouwbaarheidsniveau βg voor grondmechanisch bezwijken. Uitgaande van deze gegevens wordt een verdelingsfunctie voor de totale energie in het bezwijkmechanisme bepaald, en een waarde voor de totale energie bij gemiddelde parameters φa en ca. Met deze gegevens wordt de grondvergelijking opgesteld. Dit resulteert in de benodigde stabiliteitsfactor Fsa. Tot slot wordt in SOMARBEID op iteratieve wijze de veiligheidsfactor Fv bepaald, welke nodig is om aan het betrouwbaarheidsniveau βg te voldoen.