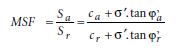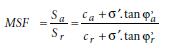Samenvatting theoretische achtergrond Methode Bakker
In dit deel is de theoretische achtergrond van de in dit rapport genoemde Methode Bakker kort samengevat. Voor een uitgebreide behandeling wordt verwezen naar [6]. Het hier als eerste behandelde deel beschrijft enkele aspecten van de gevolgde probabi- listische aanpak. In het tweede deel worden de drie voor de berekeningsmethode benodigde spreadsheets beschreven. Voor de praktische toepassing van de methodiek wordt verwezen naar het voorbeeld in appendix H.
Inleiding
De methode is een benaderende probabilistische “eerste orde tweede moment” betrouw- baarheidsanalyse voor geotechnische constructies, waarbij op onderdelen (met name spreadsheet UNDRAINE) gebruik gemaakt wordt van de principes van een “design point”-benadering [56]. De methodiek geldt voor een meerlagen ongedraineerde grondslag en is in principe ook voor andere geotechnische constructies algemeen toepasbaar. In deze appendix is de uitwerking toegespitst op kistdammen. Met de methodiek kunnen constructies ontworpen worden op een vooraf vastgesteld betrouw- baarheidsniveau. Dit betreft zowel het betrouwbaarheidsniveau van de constructie als de betrouwbaarheidsniveaus van de onderdelen. Globaal wordt als volgt te werk gegaan:
- kies betrouwbaarheidsniveau bk voor de gehele kistdamconstructie; bepaal hieruit de faalkansruimte Pfk voor de hele kistdam;
- deel deze faalkansruimte op in faalkansen voor grondbreuk, damwandbreuk links, damwandbreuk rechts en ankerbreuk; bepaal hieruit de betrouwbaarheidsniveau’s βg, βd;l, βd;r en ba voor deze deelmechanismen;
- ontwerp op iteratieve wijze volgens de Methode Bakker een kistdam- of diepwand- constructie met gegeven grondopbouw en belastingen zodanig dat aan het betrouw- baarheidsniveau voor grondbreuk βg wordt voldaan.
De methodiek maakt gebruik van het eindige-elementenprogramma PLAXIS. Ten opzichte van een quasi designpoint analyse [zie 56] heeft de methodiek het voordeel dat een relatief gering aantal PLAXIS-berekeningen nodig zijn. Voor een efficiënte toepassing zijn drie spreadsheet-modellen ontwikkeld namelijk UNDRAINE, ARBEID en SOMARBEID.
Gecombineerde faalfuncties voor meerdere bezwijkmechanismen
Een faalfunctie (Z) is een wiskundige weergave van een bezwijkmechanisme. De bezwijkmechanismen behorende bij een kistdamconstructie zijn: grondmechanisch bezwijken, damwandbreuk en ankerbreuk. Behalve voor afzonderlijke bezwijkmecha-nismen kunnen ook gecombineerde faalfuncties voor meerdere bezwijkmechanismen worden bepaald. Ter verduidelijking is in de navolgende figuur voor een uit één damwand bestaande constructie in de kansruimte de gecombineerde faalfunctie voor grondmechanisch bezwijken en damwandbreuk weergegeven. De faalfuncties luiden in dit geval:
Zg = Fs- 1
Zd = fy - fbel
Hierin zijn Zg en Zd de faalfunctie voor grond respectievelijk damwand, Fs de grond-sterkte uitgedrukt in de stabiliteitsfactor, ƒy de damwandsterkte uitgedrukt in vloei- of breukgrens en ƒbel de maximale spanning in de damwand als gevolg van belasting op de constructie.
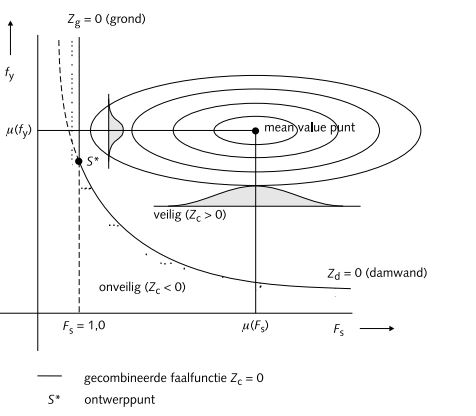
Figuur 1 Gecombineerde faalfunctie
Het zal duidelijk zijn dat voor Fs kleiner dan 1,0 grondmechanisch bezwijken optreedt, ongeacht de sterkte van het damwandmateriaal. De faalfunctie voor damwandbreuk is iets gecompliceerder. Naarmate de constructie een kleinere stabiliteitsfactor Fs heeft wordt het buigend moment in de damwand groter (zie de lijn Zd = 0).
De curve Zd = 0 en de lijn Zg = 0 snijden elkaar in het punt S*. De overblijvende (dikge- drukte) delen van Zg = 0 en Zd = 0 vormen de gecombineerde faalfunctie Zc voor damwandbreuk en grondmechanisch bezwijken voor Z = 0. In het vervolg wordt S* aangehouden als het ontwerppunt voor zowel grond-, damwand- en ankerbreuk daar deze zich in de nabijheid bevindt van de meest waarschijnlijke combinatie van Fs en fy waarbij een bezwijkmechanisme ontstaat.
In de kansruimte van figuur 1 kunnen 3 gebieden worden onderscheiden:
gebied 1: Zg > = 0 en Zd > = 0: veilig gebied 2: Zg < 0: primair zuiver grondmechanisch bezwijken(eventueel secundair damwandbreuk) gebied 3: Zg > = 0 en Zd < = 0: primair damwandbreuk (partieel grondmechanisch bezwijken)
In een niveau 2 berekening is het niet mogelijk om de kansen van de gebieden en de faalkansen exact te berekenen. In de te behandelen niveau 2 methode wordt hiertoe de faalfunctie voor damwandbreuk gelineariseerd in S*. De faalkansen worden op deze manier benaderd. In vergelijking met de exacte faalkansen treden hierbij fouten op. Met de benaderde faalkansen van de afzonderlijke onderdelen (hier aangegeven met Pf *) is een onder- en bovengrens voor de exacte faalkans van een kistdam (Pfk) te bepalen met behulp van de volgende ongelijkheden:
Max (Pf*d;l, Pf*a, Pf*d;r) < Pfk < Pf*d;l +Pf*a + Pf*d;r + Pf*g
Uitgangspunten
De volgende uitgangspunten worden in het vervolg gehanteerd: Algemeen
- Ongedraineerd grondgedrag
- Voor de bepaling van de krachtsverdeling en de relatie tussen de krachtsverdeling en stabiliteitsfactor in de buurt van grondmechanisch bezwijken wordt de methode van φ’/c’- reductie toegepast.
- De stabiliteitsfactor, veiligheidsfactor en het betrouwbaarheidsniveau βg worden bepaald uit de in het bezwijkmechanisme gedissipeerde energie na φ’/c’-reductie.
De drie bezwijkmechanismen zijn ongecorreleerd.
Deterministische parameters
- Geometrie van de constructie
- Volumegewichten en uitwendige belastingen
- Freatische lijnen, waterspanningen en grondwaterregiem
- Elastische parameters (grond, damwanden en ankers)
Stochastische parameters
- Sterkte
- Wandwrijving
- Laagscheidingsniveaus
- Vloei- of breukgrens van damwand en ankers
Voor alle stochastische parameters is aangenomen dat deze normaal (Gaussisch) verdeeld zijn.
Door de aanname dat de bezwijkmechanismen ongecorreleerd zijn, kan een bovengrens voor de faalkans van de kistdam nader bepaald worden.
Relatie tussen stabiliteitsfactor en veiligheidsfactor voor grondmechanisch bezwijken
De definitie van de stabiliteitsfactor Fs die wordt toegepast bij glijcirkelberekeningen voldoet niet bij niet-cirkelvormige bezwijkmechanismen. Voor dat geval kan Fs worden gedefinieerd als de verhouding tussen de in het bezwijkmechanisme gedissipeerde arbeid bij de aanwezige ongedraineerde schuifsterkte (E) en de in het bezwijkmecha-nisme gedissipeerde arbeid bij de ongedraineerde schuifsterkte waarbij de constructie grondmechanisch bezwijkt (Ec).

In PLAXIS wordt niet gerekend met een stabiliteitsfactor maar met een veiligheidsfactor bij het gewenste betrouwbaarheidsniveau, MSF. De veiligheidsfactor is gedefinieerd als de verhouding tussen de aanwezige gedraineerde schuifsterkte (Sa) en een gereduceerde gedraineerde schuifsterkte (Sr), zie [11].
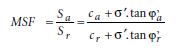
In [6] wordt aan de hand van het Mohr-Coulomb criterium een relatie tussen Fs en MSF opgesteld met behulp van de gedraineerde sterkteparameters c en φen de ongedraineerde schuifsterkte fundr. Voor een homogene grondslag is φ‘a constant over de dwarsdoorsnede en geldt:
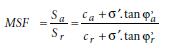
Hierin is MSFc de veiligheidsfactor bij grondmechanisch bezwijken bij het gewenste betrouwbaarheidsniveau. Voor de uitwerking van de damwandvergelijking en de anker- vergelijking blijkt ook de afgeleide δFv/δFs in het ontwerppunt voor grondmechanisch bezwijken nodig te zijn (zie [6]).