Samenvatting theoretische achtergrond Methode Bakker - Bijlagen

Energie kinematische elementen

Bij een niet-homogene grondslag is het bezwijkmechanisme verdeeld over meerdere grondlagen. In iedere grondlaag kunnen één of meer deelmechanismen optreden. De verschillende deelmechanismen zijn:

• plastische vervormingen in het grondcontinuüm;
• discrete afschuiving;
• wandwrijving

Daarnaast zijn de laagscheidingen van invloed op de energie in het bezwijkmechanisme. Met name gaat het om de onzekerheid in de ligging van de laagscheidingen.

Deze deelmechanismen kunnen, afhankelijk van de vorm van het bezwijkmechanisme, worden opgedeeld in een samenstel van kinematische elementen van grondelementen, schuifvlakelementen en wandwrijvingselementen, zie figuur 2.

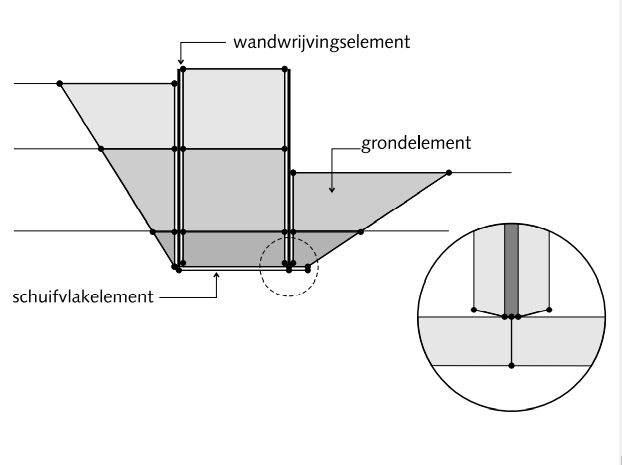
Figuur 2 Kinematische elementen

Voor deze kinematische elementen dient de energie in het bezwijkmechanisme te worden bepaald. De energie in een kinematisch element is de integraal over het kinematisch element van het product van schuifrekken en schuifsterkte (voor uitwerking zie [6]).

Voor de laagscheidingsniveaus geldt dat deze alleen een bijdrage levert aan de energie in het bezwijkmechanisme wanneer het werkelijke niveau afwijkt van het niveau waarvoor de indeling in kinematische elementen is bepaald.

Voor het opstellen van een probabilistische beschouwing van de energie in het bezwijk-mechanisme moeten de verdelingsfuncties van de energie in de kinematische elementen (en in de laagscheidingen) bekend zijn.

Grond-, damwand- en ankervergelijking

De grondvergelijking kan worden afgeleid uit de faalfunctie voor grondmechanisch bezwijken Zg.

Deze functie is een functie van de energie in het bezwijkmechanisme.

Deze energie is op zijn beurt een functie van de ongedraineerde schuifsterktes fundr in de kinematische elementen. Deze laatste zijn een functie van de gedraineerde sterkte- parameters c’ en φ‘ in de kinematische elementen. De laatste functie is niet lineair.

Voor de bepaling van het gemiddelde µ (Fs), de standaardafwijking σ (Fs) en het betrouwbaarheidsniveau voor grondmechanisch bezwijken βg wordt Zg gelineariseerd in het ontwerppunt S* (zie figuur 1).

Uit de faalfunctie volgt vervolgens de stabiliteitsfactor Fsdie nodig is om aan het vereiste betrouwbaarheidsniveau βg te voldoen. Omdat de vorm van het bezwijkmechanisme vooraf niet bekend is, en ook niet bekend is welke veiligheidsfactor MSF voor het betrouwbaarheidsniveau noodzakelijk is kan Fsalleen iteratief bepaald worden. Een eerste schatting voor Fskan worden gedaan uitgaande van µ (fundr) en σ (fundr) berekend met de gemiddelde waarden van de sterkteparameters c’aen φ’a (dit zijn de reken- waarden van de in situ aanwezige sterkteparameters.

De damwandvergelijking kan worden afgeleid uit de faalfunctie voor damwandbreuk Zd. Deze is een functie van het opneembare damwandmoment en het in de constructie optredende moment. Deze laatste is een functie van de aanwezig grondsterkte. De aanwezige grondsterkte kan uitgedrukt worden in Fs. De relatie tussen het optredende moment en Fsis niet-lineair. De relatie kan worden bepaald met φ’/c’-reductie met PLAXIS. Tijdens het reduceren van φ’ en c’ nemen de belastingen op de damwanden toe, en daardoor worden de buigende momenten in de damwanden steeds groter.

Voor de bepaling van het gemiddelde µ (MY;dam), de standaardafwijking σ (MY;dam) en het betrouwbaarheidsniveau voor grondmechanisch bezwijken βd wordt Zd gelineari- seerd in het ontwerppunt S* (zie figuur 1).

De ankervergelijking kan worden afgeleid uit de faalfunctie voor ankerbreuk Za. Deze faalfunctie is een functie van de opneembare ankerkracht en de in de constructie optre- dende ankerkracht. Deze laatste is een functie van de aanwezige grondsterkte. De uitwerking van de ankervergelijking is analoog aan die voor de damwandvergelijking.

Spreadsheet-modellen

Voor de toepassing van de voorgaande beschreven probabilistische aanpak zijn drie spreadsheet-modellen ontwikkeld namelijk UNDRAINE, ARBEID en SOMARBEID.

UNDRAINE

In UNDRAINE wordt een probabilistische niveau 2 analyse uitgevoerd voor de ongedraineerde schuifsterkte fundr. Daarbij wordt gebruik gemaakt van een niveau 2 quasi designpoint analyse zoals beschreven in [56].

De volgende gegevens zijn benodigd:

• Verdelingsfuncties van c’ (µ en σ)en φ’ (µ en σ)
• Wandwrijvingscoëfficiënt Rw
• Veiligheidsfactor MSF
• Effectieve korrelspanningen (K0 en σ1)

Na de berekening verschijnen in het spreadsheetmodel UNDRAIN de volgende, voor het spreadsheetmodel ARBEID benodigde, grootheden:

• Verdelingsfunctie van fundr (µ en σ)volgens een linearisatie in het ontwerppunt en fundr;a

De berekening is een iteratief proces. De eerste iteratie is een zogenaamde mean value berekening. Dit resulteert in een eerste schatting van het ontwerppunt. In volgende iteraties wordt het ontwerppunt steeds verder verbeterd. Het is gebleken dat 4 iteraties hiervoor meer dan voldoende zijn.

ARBEID

In het spreadsheetmodel ARBEID wordt de energie in een kinematisch element geïnte- greerd. Daarbij wordt gebruik gemaakt van isoparametrische elementenformulering zoals beschreven door Bathe [7]. De integratie van oppervlakte-integralen wordt uitge- voerd door middel van numerieke integratie met naar keuze 4 of 9 integratiepunten. De randintegralen worden met 2 integratiepunten uitgevoerd. Een nadere uitwerking van de elementenformulering wordt hier achterwege gelaten. Er kunnen vierknoops elementen van willekeurige vorm worden geïntegreerd. Dit impliceert dat de rekken en schuifsterkten lineair over het element worden geïnterpoleerd. De in het eerste deel beschreven integralen over het kinematisch element ter bepaling van de energie hierin

kunnen allen met ARBEID worden bepaald. De integratie moet worden uitgevoerd voor

µ (fundr), σ (fundr) en fundr ;a.

Kort gezegd berekent ARBEID de verdelingsfunctie E (µ ,σ)voor een specifiek kinematisch element en/of laagscheidingen. Hiervoor dienen de volgende gegevens te worden ingevoerd:

• Geometrie van het kinematisch element (hoekpunten)
• Verdelingsfunctie fundr (µ ,σ)
• Verplaatsings-incrementen
• Standaardafwijkingen van de laagscheidingsniveaus

Dit resulteert in de volgende, voor het spreadsheet SOMARBEID benodigde, grootheden:

• Verdelingsfunctie van de energie E (µ,σ)
• Waarde voor de energie bij gemiddelde parameters 

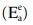
SOMARBEID

In het spreadsheetmodel SOMARBEID worden de met het spreadsheetmodel ARBEID berekende energieën van de afzonderlijke kinematische elementen gesommeerd tot de totale energie in het bezwijkmechanisme. Uit deze sommatie volgen drie factoren voor de grondvergelijking namelijk Ea ,µ (E), σ (E). De evaluatie van de grondvergelijking resulteert in de benodigde stabiliteitsfactor Fs. Daarnaast vindt ook een bepaling plaats van de energie Ec waarbij de constructie bezwijkt. De energie Ec is nodig voor de itera- tieve bepaling van de veiligheidsfactor Fv (als functie van Fs), daar in PLAXIS gerekend wordt met een veiligheidsfactor Fv = MSF. Voor het oplossen van de damwandverge- lijking en de ankervergelijking geeft het spreadsheet de afgeleide δFv/δFs . Ten behoeve van de voornoemde berekening zijn de verdelingsfuncties van de energie E(m,s)voor alle kinematische elementen en laagscheidingen benodigd alsmede het betrouwbaar- heidsniveau βg voor grondmechanisch bezwijken.