Lengte-effect - Veiligheidsbenadering ten aanzien van ontwerp en toetsing

Lengte-effect

Bij langgerekte constructies, zoals waterkeringen, is de faalkans ruwweg evenredig met de lengte van de beschouwde strekking.

De betrouwbaarheidseis (de minimale vereiste β) voor de gehele strekking moet dan worden vertaald in een betrouwbaarheidseis voor een “doorsnede”; immers voor de doorsnede worden ontwerpberekeningen gemaakt. In die vertaalslag speelt de mate van variabiliteit van de ontwerpparameters in de doorsnedeberekening een belangrijke rol. Meestal zijn dit geometrieparameters of parameters die de grondeigenschappen beschrijven.

De vertaalslag resulteert in een benodigde β voor een doorsnede die groter is dan de β voor de gehele strekking.

Het verband tussen βnodig en de lengte van de strekking is niet in een eenvoudige relatie uit te drukken. Dit verband is bovendien afhankelijk van het betreffende faalmecha- nisme en van het ruimtelijk variatiepatroon van belasting en sterkte. De figuur 4.2, die is ontleend aan het Handboek Damwandconstructies [19], kan dienen als een eerste benadering van het lengte-effect. Indien de waarde van βnodig bij een gegeven strekkings- lengte L niet op de lijn ligt die in figuur 4.2 is aangegeven, kan als benadering voor het verband tussen en L een verloop van de lijn worden aangehouden evenwijdig aan de lijn in figuur 4.2.

In gevallen waarin het ontwerp van de kistdam of diepwand voor een strekking wordt gebaseerd op het ongunstigste dwarsprofiel (bijvoorbeeld diepste gedeelte rivierbodem, slechtste sondeerwaarde etc.) binnen de strekking, zal de faalkans vrijwel uitsluitend bepaald worden door die doorsnede. De overige delen van de strekking leveren dan weliswaar bijdragen aan de faalkans maar die vallen in het niet bij de bijdrage van de extreem ongunstige doorsnede. In zo’n geval kan compensatie van de vereiste βvoor lengte-effecten volledig achterwege worden gelaten.

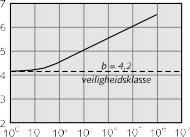
Figuur 4.2 Invloed van de strekkingslengte op de vereiste b-waarde voor een damwand in veiligheidsklasse 3 [19]