Rekenmodel voor verticale piping
Voor verticale uitspoeling van zand bij verticaal gerichte opwaartse stroming benedenstrooms van een kwelscherm bestaan geen gangbare rekenmodellen. Reden hiervoor is dat dit mechanisme niet als maatgevend wordt beschouwd. In proeven is aangetoond dat als het uittredeverhang voor heave kritiek is, er van het uitspoelen van zandkorrels (piping) nog lang geen sprake is.
Bij goed functionerende kwelschermen lijkt dit een juiste veronderstelling. Echter, in geval van geconcentreerde lekkage van het kwelscherm wordt het risico op instabiliteit van het kwelscherm ten gevolge van heave veel geringer. Dan zou verticale piping opeens maatgevend kunnen worden, met name als er sprake is van een gat dat vrij hoog in het kwelscherm zit en de verticale kwelweg kort is. Een toetsregel bestaat daarvoor niet. De regel van Sellmeijer heeft alleen betrekking op horizontale piping.
Zoals vermeld is het verticale verhang dat noodzakelijk is voor het uitspoelen van zandkorrels groter dan dat voor fluïdisatie .Zie ook [Van Rossum & Zanen, 1959]. Er kan dus vanuit worden gegaan dat de korrels al in suspensie zijn voordat piping begint. Dat betekent dat gesteld mag worden dat de zandkorrels naar boven kunnen uitspoelen als de verticaal gerichte opwaartse stroomsnelheid groter wordt dan de bezinksnelheid van de korrels.
De bezink- (of sedimentatie-)snelheid (v) van korrels ten gevolge van alleen de zwaartekracht kan met de wet van Stokes worden benaderd met:
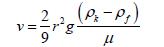 (5.16)
(5.16)
waarin:
v sedimentatiesnelheid van het gronddeeltje [m/s] r straal (sferisch) gronddeeltje [m]
r straal (sferisch) gronddeeltje [m]
Ρk dichtheid van het gronddeeltje [kg/m3]
Ρf dichtheid van de vloeistof [kg/m3]
g zwaartekrachtversnelling [m/s2]
μ dynamische viscositeit van de vloeistof [kg/m·s]
Onderstaand rekenvoorbeeld geeft aan welk verticaal uittredeverhang ongeveer nodig zou zijn voor uitspoeling van zandkorrels:
Bij een korreldiameter van 150 μm (fijn zand) wordt met bovenstaande vergelijking v = 0,02 m/s. Voor verticale uitspoeling van zand moet de verticaal gerichte opwaartse effectieve snelheid van het grondwater dus minimaal die waarde hebben. Uitgaande van een zeer hoog poriëngehalte van 0,5 (zo ongeveer de meest losse pakking) betekent dit dat de kritieke filtersnelheid 0,04 m/s is. De doorlatenheidscoëfficiënt kan berekend worden met (bijvoorbeeld) de vergelijking van Kozeny-Carman:
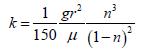 (5.17)
(5.17)
Met n = 0,5 levert dit k = 1,3·10-3m/s. Met de wet van Darcy kan nu het kritieke verhang berekend worden: ic= 0,04 / 1,3·10-3≈ 30. Dit is een factor 30 hoger dan het kritieke verhang voor heave.
Hierbij is uitgegaan van een (weinig realistische) uniforme korrelverdeling en een volledig gelijkmatige verticaal gerichte opwaartse grondwaterstroming. Gezien het hoge kritieke verhang is in dat geval het optreden van verticale piping dus vrij onwaarschijnlijk. De grond
zal wat betreft doorlatendheid zeker niet homogeen zijn, waardoor de grondwaterstroming zich zal concentreren en locaal veel hogere stroomsnelheden ontstaan. Indien piping optreedt zal de doorlatendheid en daarmee de stroomsnelheid verder toenemen. Of daarin dergelijk hoge benodigde stroomsnelheden als in bovenstaand voorbeeld kunnen ontstaan is er sterk van afhankelijk of vanuit het omringende zand voldoende water kan toestromen.
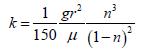 (5.17)
(5.17)