Niet-stationaire benadering met behulp van de transiente lekfactor (bij par. 2.3.6) - Bijlage 3

Niet-stationaire benadering met behulp van de transiënte lekfactor (bij par. 2.3.6)

Het is mogelijk om via peilbuiswaarnemingen direct de maatgevende modelparameters vast te stellen, waarbij de invloed van de aanwezige heterogeniteit automatisch is verdisconteerd. De methode berust op calibratie van peilbuiswaarnemingen gedurende de hele hoogwaterperiode en enige tijd erna (model 3C). Hierbij is het tijdsafhankelijk gedrag essentieel. Het model dat wordt gehanteerd, is gebaseerd op de theorie van de transiënte lekfactor [Barends, 1982]. Door calibratie over het hele traject zijn de geohydrologische (veld)parameterwaarden te bepalen: de lekfactoren in voor- en achterland, en met aanvullende informatie ook de transmissiviteit van het watervoerend zandpakket (kD-waarde), de hydraulische weerstand van de toplaag (D'/k') en de “consolidatiecoëfficiënt bij zwel” c' van de toplaag. In sommige gevallen kan ook de berging van het zandpakket worden meegenomen (S = cv/kD, cv= consolidatiecoëfficiënt van het zandpakket), maar in de meeste gevallen is deze parameter niet essentieel.

Het model is te ingewikkeld voor handberekening. Er is in opdracht van Rijkswaterstaat door GeoDelft een gebruikersvriendelijk PC-programma ontwikkeld: WATEX. Met dit programma kan voor een aantal specifieke situaties op eenvoudige wijze een berekend stijghoogteverloop in overeenstemming worden gebracht met een gemeten verloop door iteratief de meest geschikte geohydrologische parameterwaarden in te voeren. Omdat het mogelijk is dat verschillende sets parameters een “juiste” uitkomst geven, is hierbij wel goede kennis van geohydrologie nodig. Is eenmaal de geohydrologie bepaald, dan kan vervolgens met het programma de tijdsafhankelijke stijghoogte onder maatgevende hoogwaterstanden worden berekend. In het programma kan rekening worden gehouden met eventuele aanwezigheid van voorland en achterland, waar de geohydrologische structuur anders kan zijn. Ook is het mogelijk om meerdere watervoerende lagen te beschouwen.

De methode van de transiënte lekfactor is gebaseerd op superpositie van elementaire belastingstappen, die met Laplace transformatie voor geschematiseerde geohydrologische systemen zijn bepaald. In de systemen is het mogelijk om onderscheid te maken in voor- en achterland, en in een of twee zandvoerende lagen met semi-doorlatende toplaag en tussenlaag. Het superpositiebeginsel (convolutie) maakt een willekeurig tijdsgedrag toepasbaar (dus voor hoogwatergolven in het bovenrivierengebied, voor hoogwater en getijde in het benedenrivierengebied en voor stormvloed in het kustgebied), maar niet lineaire effecten (freatische stijging, opdrijven) kunnen niet worden meegenomen. Naast het ijken van peilbuiswaarnemingen over de hele hoogwaterperiode, is het model (WATEX) eenvoudig geschikt om te extrapoleren naar maatgevende ontwerpomstandigheden met een eigen hoogwaterverloop.

Door ijking van peilbuiswaarnemingen over het hele tijdstraject zijn iteratief de regionale karakteristieke geohydrologische parameters vrij nauwkeurig vast te stellen, uiteraard afhankelijk van de toepasbaarheid van de geologische schematisering. Als vanzelf komen nu inloop- en uitloopeffect, demping en vertraging tot uiting.

Bovendien is het mogelijk ook de waterdrukontwikkeling in de semi-doorlatende lagen in de tijd te berekenen. In figuur b3.14 is een voorbeeld gegeven van een berekening voor een hypothetische situatie belast door een twee- toppige hoogwatergolf. De verschillende hoogwatertoppen veroorzaken ieder hysteresislussen (ellipsachtige vormen) Ook is in dit geval de uitloop herkenbaar.

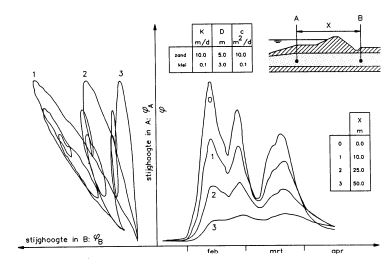
Figuur b3.14 Stijghoogte-respons; hoogwatergolf 1947-1948

Interpretatie van peilbuiswaarnemingen i.g.v. onderstroming van hoog voorland (bij par. 2.3.6)

In figuur b3.15 is een geschematiseerde situatie gegeven van een dijk met hoog voorland.

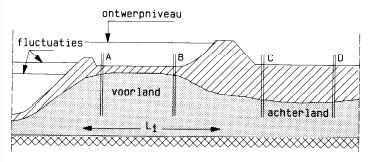
Figuur b3.15 Rivierdijk met hoog voorland

Bij het onderlopen van voorland tijdens hoogwater is de situatie wezenlijk anders dan tijdens normale omstandigheden, wanneer de rivier in het zomerbed blijft. Bij de metingen moet hier rekening mee worden gehouden (model 3E). Niettemin is een peilbuismeting tijdens normale omstandigheden te gebruiken voor ontwerpomstandigheden met ondergelopen voorland, door gebruik te maken van de methode van cyclische of transiënte lekfactor. In het model WATEX is daartoe een drie-sectie situatie opgenomen.

Situatie bestaat uit 3 secties:

• rivierbed (met sliblaag)        λ”
• voorland (met toplaag)        λ’
• achterland (met toplaag)    λ

Voor dit drie-sectie systeem is een fundamentele oplossing afgeleid. De gevonden uitdrukkingen zijn gecompliceerd en niet geschikt voor een eenvoudige toepassing. Voor willekeurige rivierstand (in het zomerbed) kan met WATEX een peilbuismeting uitgewerkt worden (kalibreren van gekozen materiaalparameters).

Een vereenvoudigde aanpak is in sommige situaties mogelijk met behulp van cyclische lekfactoren, daarbij gebruikmakend van de in deze bijlage gepresenteerde formules. Het systeem wordt daarbij opgedeeld in twee subsystemen:

• rivier en voorland                λω”
• voorland en achterland     λω’

In het voorland en achterland worden in totaal 4 peilbuizen geplaatst, zoals in de figuur b3.15 is aangegeven. Peilbuizen A en B worden gebruikt om voor wisselingen in het zomerbed (droog voorland) de weerstand van rivierbodem en voorland vast te stellen. De hiervoor beschreven methode levert λω” en λω’

.Hierbij wordt verondersteld dat het achterland identieke eigenschappen bezit als het voorland. Als het voorland een lengte van betekenis heeft, dan is deze aanname gerechtvaardigd. Als criterium kan worden gesteld dat het achterland nauwelijks invloed heeft, als geldt dat de lengte van het voorland groter is dan de gevonden cyclische lekfactor:

L > λω’

.Vervolgens worden resultaten van peilbuis C en D benut om λω’ te bepalen. De gevonden waardenλω’ en λω" zijn nu te gebruiken voor de analyse van het ontwerpniveau. Vanwege het onder water komen van de droge toplaag in het voorland wordt een extra weerstand (luchtinsluitingen) gemobiliseerd. In de hier gesuggereerde aanpak is die niet meegenomen.

Een complicatie vormt het feit dat het consolidatiegedrag in het voorland bij ontwerphoogwater wordt bepaald door compressie terwijl het in het achterland wordt bepaald door zwel. Compressie en zwel hebben te maken met respectievelijk belasten en ontlasten. De samendrukbaarheid van samendrukbare grond bij belasten is significant groter dan bij ontlasten. Derhalve is de λω’ waarin de samendrukbaarheid  α voorkomt onder een 4e machtswortel:

λω’(:) 1/4√α, anders bij de bepaling met zomerpeilfluctuaties dan bij ontwerphoogwater.

Echter de samendrukbaarheid wijkt bij herbelasten weinig af van de waarde bij ontlasten. Bovendien zal het meestal zo zijn, dat de belasting boven de historisch extreme waarde gering is. Daarnaast wordt het feitelijk verschil in λω’ gereduceerd door de 4e machtswortel. Een orde van grootte van het effect van belasten boven de historisch extreme waarde zal daarom gering zijn.

In de literatuur [Bauduin & Barends, 1987] is een specifieke situatie uitgewerkt aan de hand van peilbuismetingen (zie figuur b3.16) voor een dijk met voorland. Uit de metingen is te zien dat er sprake is van significante demping, maar – vreemd genoeg – nauwelijks van vertraging (door volstromen van voorland vindt er een negatieve voorijling plaats). Het resultaat van de analyse in deze case/studie is een voorlandfactor van 90 m en een achterlandfactor van 300 m. Met deze informatie kan nu een willekeurige ontwerpsituatie worden geanalyseerd.

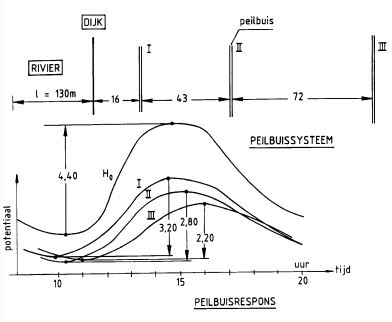
Figuur b3.16 Gemeten hoogwater in een dijkraai met voorland [Bauduin & Barends, 1987]