Methode met gebruikmaking van de cyclische lekfactor m.b.v. een 13-uurs meting (bij par. 2.3.6) - Bijlage 3

Door het seizoeneffect zal de gemiddelde (semi-)stationaire stijghoogte in het watervoerend pakket 's winters hoger zijn dan in de zomer. Meestal zijn ook maatgevende hoogwaterstanden in de winter te verwachten. Dus peilbuiswaarnemingen kunnen het best 's winters worden uitgevoerd (zie figuur b3.10).

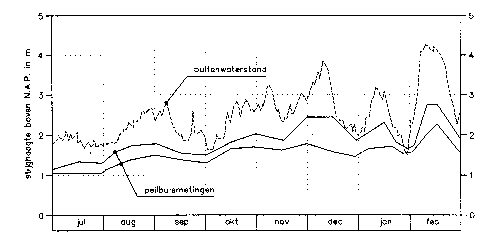
Figuur b3.10 Effect van de seizoenen op de gemiddelde stijghoogte

Voor zeedijken wordt in Basisprincipes van de kustwaterbouw II, Getijden en getijstromen [Verhagen & Roelse, 1988] de achtergrond van getijdebewegingen beschreven. Aan de hand van Getijdetafels voor Nederland [SDU] kan een tijdstip worden gekozen, waarop het getij maximaal is.

In principe is de methode van de cyclische lekfactor geschikt voor het benedenrivierengebied en het overgangsgebied, waar getijde-effecten nog goed meetbaar zijn. Het bovenstaande maakt aannemelijk, dat het niet nodig is een permanent meetsysteem van peilbuizen te hanteren. Eenmalig nauwkeurig vaststellen van de karakteristieke modelparameter (lekfactor) volstaat. Hierbij moet echter worden bedacht, dat de bergingscapaciteit kan veranderen afhankelijk van de absolute waarde van het hoogwater door geometrische effecten (voorland, grenspotentiaal) of fysische effecten (luchtinsluiting, niet-lineaire compressibiliteit en doorlatendheid) en tenslotte ook door de complexiteit van de werkelijkheid (3-dimensionaal, heterogeniteit). In die gevallen is inzicht en ervaring nodig om te onderbouwen dat de gekozen aanpak een veilige is.

Zoals al eerder gesteld is het in principe mogelijk rekening te houden met een hoogwatergolf die lijkt op een halve sinusboog [GeoDelft, 1986]. Hoe dat in zijn werk gaat wordt hieronder uiteengezet.

Als een peilbuismeting wordt uitgevoerd gedurende een hoogwatergolf, bijvoorbeeld in het bovenrivierengebied waar het geologisch profiel overeenkomst vertoont met het Hollandprofiel (een zandpakket afgedekt door een semi- doorlatende toplaag), dan ziet de curve die het verband aangeeft tussen de meting en de buitenwaterstand er theoretisch uit als een ellips met enige afwijkingen in de oorsprong (zie figuur b3.11).

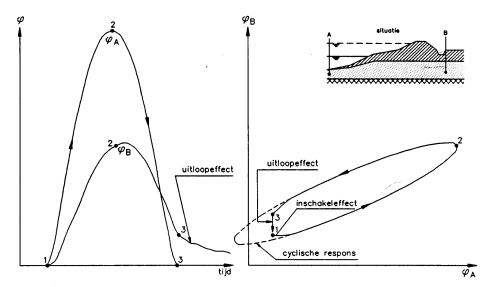
Figuur b3.11 Schematische hoogwater respons

Bij de start van de hoogwatergolf (punt 1) wordt het stijghoogteverloop in de peilbuis bepaald door het inloop effect. Dit is meestal van korte duur, afhankelijk van de afstand tussen de peilbuis en de rivier (intreepunt). Vervolgens verloopt het beeld, zoals dat te verwachten is, gedempt met relatief weinig vertraging. Na de hoogwatergolf (vanaf punt 3) vertoont het potentiaalbeeld een sterke vertraging, het zogeheten uitloopeffect. Bij continue cyclische waterstandsfluctuaties is dit effect niet zichtbaar.

Het uitloopeffect laat zien dat na het hoogwater (vanaf punt 3) er nog langere tijd enige wateroverspanningen aanwezig zijn.

De situatie na hoogwater kan daarom wel ongunstig zijn voor de stabiliteit, met name als er snel opvolgend een nieuwe hoogwatergolf volgt. De bergingscapaciteit is dan geringer en hoge waterspanningen worden sneller bereikt. In figuur b3.12 is dat weergegeven

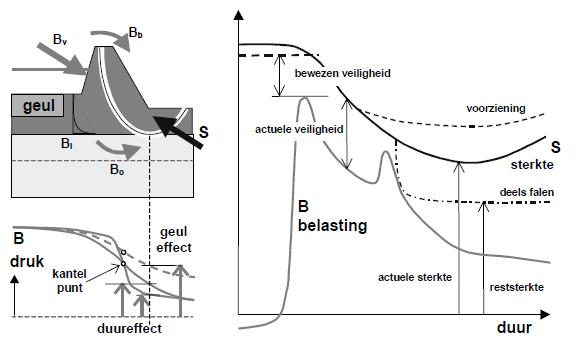
Figuur b3.12 De sterkte van een dijk bij meervoudig hoogwater

In de rechterfiguur is de belasting door hoogwater aan de voorkant van de dijk (B) en de sterkte (S) uitgezet als functie van de tijd. Tijdens een hoogwater neemt de sterkte af door het verzadigd raken van de dijk. Dit gebeurt op verschillende manieren: bovenbelasting door overloop (Bb), interne consolidatie (Bi), onderstroom en opdrijven (Bo). Linksonder is de ontwikkeling van de stijghoogte in het zandpakket geschetst, waarbij de verschuiving van het kantelpunt in de tijd en bovendien het effect van een eventuele geul is aangegeven, ter plaatse van een mogelijke opdrijfzone (onderkant van de afschuifzone). Deze effecten kunnen met beschikbare modellen (WATEX, PLAXIS) worden gemodelleerd.

Bij toenemende waterdruk is er in samendrukbare grond sprake van zwelling (mits de totaalspanning gelijk blijft). De karakteristieke parameter hierbij is de “consolidatiecoëfficiënt bij zwel”, die vergelijkbaar is met de consolidatiecoëfficiënt (bij compressie). Deze “consolidatiecoëfficiënt bij zwel” wordt kortheidshalve ook wel “zwelconstante” genoemd, maar moet niet worden verward met de “samendrukkingsconstante bij zwel”, die eveneens zwelconstante wordt genoemd, en evenmin met de “samendrukkingscoëfficiënt bij zwel”. Het meten van de “consolidatiecoëfficiënt bij zwel” kan niet zonder meer met de gebruikelijke samendrukkingsproef in het laboratorium. In 1992 is een aparte meetopstelling gebouwd om de “consolidatiecoëfficiënt bij zwel” onder diverse omstandigheden te bepalen. Op een beperkt aantal kleimonsters is vervolgens een serie proeven uitgevoerd. Hieruit is vast komen te staan, dat de “consolidatiecoëfficiënt bij zwel” circa zes keer groter is dan de consolidatiecoëfficiënt bij compressie. De spreiding is echter groot, zie figuur b3.13 welke afkomstig is uit “Meetopstellen ter bepaling van de zwellingsconstante” [Heidemij, 1992].

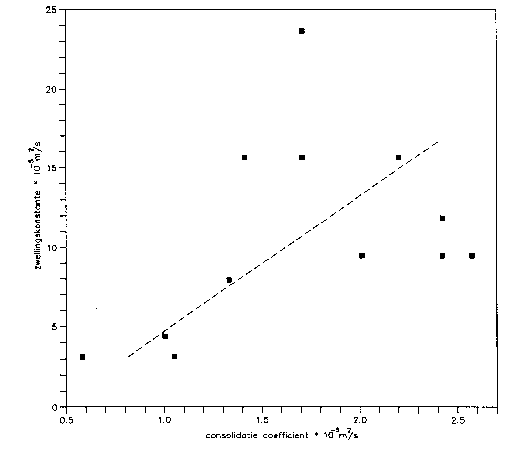
Figuur b3.13 Relatie tussen “consolidatiecoëfficiënt bij zwel” en consolidatiecoëfficiënt voor enkele kleimonsters

Aangezien de hydrodynamische periode (tijdschaal van het zwellingsproces) lineair samenhangt met de reciproke waarde van de “consolidatiecoëfficiënt bij zwel” en derhalve ook met de grootte en duur van de wateroverspanningen tijdens de uitloop, is voor de interpretatie van de tijdsafhankelijke respons een goed inzicht in de waarde van de “consolidatiecoëfficiënt bij zwel” belangrijk. Voor veel grondtypen is hierover nog onvoldoende kennis beschikbaar. De “consolidatiecoëfficiënt bij zwel”, die wordt bepaald aan de hand van laboratoriumproeven, geeft vooral informatie over het lokale gedrag en niet over het regionale gedrag. Als er sprake is van heterogeniteit (zandinsluitingen en dergelijke) is een veldwaarde maatgevend. Deze kan sterk kan afwijken van een lokale waarde. In een studie over transport in klei met zandlenzen wordt aangetoond dat de consolidatiecoëfficiënt wel een factor 100 en meer kan afwijken, afhankelijk van de mate van heterogeniteit.