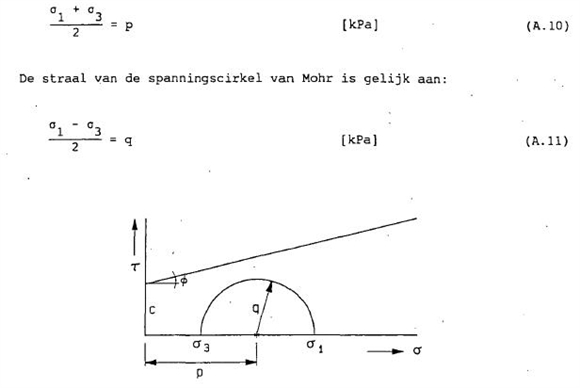
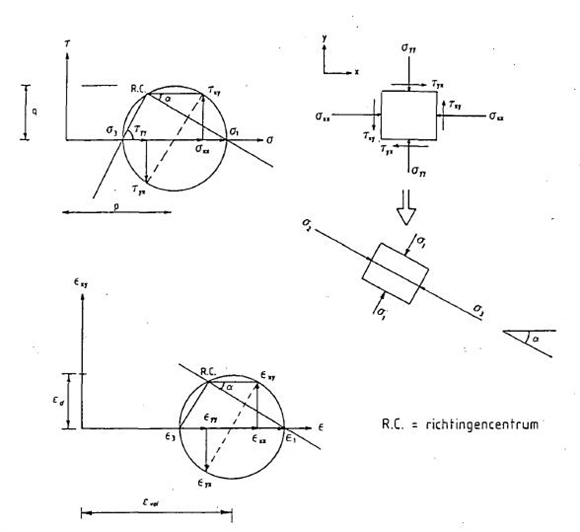
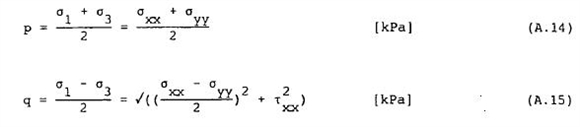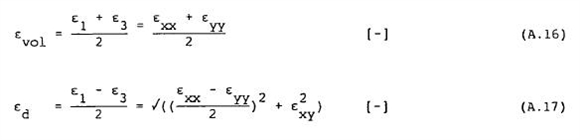Enkele basisbegrippen elasticiteitstheorie (vervolg) - Spannings-vervormingseigenschappen van grond

Het middelpunt van de spanningscirkel van Mohr is gelijk aan:

fig a10-11

Figuur A.1

Bovenstaande gegevens, gesubstitueerd in de vergelijkingen (A.4) en (A.6), leveren een eenvoudige uitdrukking op voor de spannings-rek-relaties.

fig a12-13

Vergelijking (A.2) wordt buiten beschouwing gelaten omdat alleen de vervormingen in het vlak van het dwarsprofiel van de dijk worden berekend.

Opmerkingen:

K en G kunnen direkt worden bepaald met behulp van een triaxiaalproef.
De vervormingen kunnen worden opgevat als de superpositie van een alzijdige kompressie en een hoekverdraaiing. De alzijdige kompressie komt overeen met
Tussen de hoofdspanningen en de spanningen in een voor de beschouwing aangenomen x-y-assenstelsel bestaat de volgende relatie:

fig a14-15

Ten aanzien van de vervorming bestaat een soortgelijke relatie:

fig 16-17

Verklaring:

ε_vol = volumerek [-]
ε_d = deviatorische of hoekverdraaiingsrek [-]

Dit is in figuur A.2 aanschouwelijk gemaakt met behulp van de spannings- en rekcircel van Mohr.

fig a2

figuur A.2

Bron

Hoofdstuk: Spannings- vervormingseigenschappen van grond
Auteur: Andringa R.J., P.W. Roest, R.J. Cirkel, J. Dekker, G.J. Flórián, K. de Graaf, J.H. Pool, J.J.W. Seijffert, R.J. Termaat, A. van Urk, J.G. Westerhoven
Organisatie auteur: Heidemij Adviesbureau, Rijkswaterstaat, Grondmechanica Delft, Hoogheemraadschap van de Alblasserwaard en de Vijfheerenlanden, Grontmij, Provincie Zuid-Holland
Opdrachtgever: Technische Adviescommissie voor de Waterkeringen
Verschijningsdatum: Oktober 1989
PDF: L2a_Leidraad voor het ontwerpen van rivierdijk Deel 2 - benedenrivierengebied appendices.pdf (pdf, 4 MB)

Tekst is letterlijk overgenomen uit brondocument.