Inleiding
In ENW/TAW leidraden werden en worden veiligheidseisen gerelateerd aan voor de primaire waterkeringen in de wet vastgelegde beveiligingsnormen. Die worden uitgedrukt in termen van kansen per jaar (1/10.000 tot 1/1.250) op overschrijding van hydraulische belastingen waarop de waterkeringen berekend dienen te zijn. Deze kansen worden ook wel aangeduid als normfrequenties.
De hieruit voortkomende hydraulische belastingen of belastingeffecten8 worden gecombineerd met ontwerprichtlijnen of toetsvoorschriften en bepalen zo de feitelijke doorbraakkans en daarmee de kans op overstroming9 van het achterland.
In de toekomst zullen beveiligingseisen gekoppeld zijn aan toelaatbare overstromingskansen van het achterland, gebaseerd op economische kosten/baten analyses en slachtofferrisico. Voor het afleiden van semi-probabilistische ontwerp- of toetsregels met betrekking tot specifieke faalmechanismen wordt de toelaatbare overstromingskans herleid tot toelaatbare kansen op de verschillende potentiële faalmechanismen die een rol spelen (via de ‘faalkans begroting’).
Bij het afleiden van toetsregels voor opbarsten en piping in de huidige opzet is op deze werkwijze een voorschot genomen. Als uitgangspunt is, vooralsnog, gekozen dat de toelaatbaar geachte kans op opbarsten en piping ten hoogste een tiende van de voor het beschermde gebied geldende normfrequentie mag zijn. Daarmee is de ontwerp- of toetseis bij dit faalmechanisme uitgedrukt in termen van een toelaatbare bijdrage aan de overstromingskans.
De toelaatbare bijdrage aan de overstromingskans is een kans die betrekking heeft op een periode van één jaar. Er zijn twee interpretaties denkbaar, namelijk:
-
-
dat in elk afzonderlijk opvolgend jaar de feitelijke bijdrage aan de overstromingskans door opbarsten en piping ten hoogste gelijk mag zijn aan deze kans;
- dat deze kans mag worden opgevat als toelaatbare gemiddelde faalfrequentie per jaar over een bepaalde referentieperiode. Die referentie periode kan bestaan uit een aantal jaren tot, in principe, zelfs de geplande levensduur (de planperiode)
(Voor beide interpretaties geldt dat, rekenend met een periode van N jaar, de toelaatbare bijdrage aan de overstromingskans door opbarsten (O) en piping (P) in die N jaar ongeveer N keer de toelaatbare bijdrage per jaar is. Preciezer geformuleerd: als PO+P, 1 de toelaatbare bijdrage per jaar is, dan is PO+P, N met:
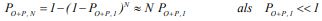 (A 1.31)
(A 1.31)
8 Bij, bijvoorbeeld, de beschouwing van macrostabiliteit van het binnentalud van een dijk is de waterstand zelf geen belasting, maar wel het effect er van op de freatische lijn of de water(over)spanning in de ondergrond.
9 Overstroming kan in beginsel ook ontstaan door overlopen van de dijk zonder dat deze doorbreekt. Vooralsnog wordt
gesteld dat overlopen van een dijk met grote debieten altijd tot dijkdoorbraak leidt
de toelaatbare bijdrage in N jaar.
Wanneer de feitelijke doorbraakkansen in de opvolgende jaren gelijk zijn en (stochastisch) onafhankelijk, dan zijn de verschillen in interpretatie van de toelaatbare doorbraakkans per jaar niet van belang. Wanneer de feitelijke overstromingskansen in opvolgende jaren gelijk zijn maar niet onafhankelijk, dan biedt de tweede interpretatie mogelijkheden tot optimalisatie.
Het gevolg van afhankelijkheid is dat de feitelijke doorbraakkans in N jaar kleiner is dan N keer de feitelijke (berekende) doorbraakkans in één jaar. In Figuur I.0.1. wordt dit geïllustreerd. In deze figuur worden op de horizontale as faalkansen uitgezet die betrekking hebben op één jaar. Op de verticale as worden bijbehorende faalkansen uitgezet, die betrekking hebben op een periode van 50 jaar. De afhankelijkheid tussen faalkansen in de opvolgende jaren wordt gereflecteerd door de correlatiecoëfficiënt ρ (rho). Bij een correlatiecoëfficiënt ρ=0 zijn de faalkansen in opeenvolgende jaren onafhankelijk van elkaar. De faalkans gedurende een periode van 50 jaar is dan (bij benadering) gelijk aan 50 keer de faalkans per jaar (bovenste lijn in de grafiek). Bij een correlatiecoëfficiënt ρ=1 zijn de faalkansen volledig afhankelijk. De faalkans gedurende een periode van 50 jaar is dan gelijk aan de faalkans per jaar (onderste lijn in de grafiek). De tussenliggende lijnen geven faalkansen weer, betrokken op 50 jaar, uitgaande van de faalkans per jaar op de horizontale as, bij correlatiecoëfficiënten van 0,7, 0,9 en 0,99. Dit zijn overigens benaderingen die berekend zijn met formule van Ditlevsen voor ondergrensschattingen. Uit de grafiek volgt dat een sterke afhankelijkheid (hoge correlatiecoëfficiënt) tussen de kansen in opeenvolgende jaren nodig is, om de kansen voor de 50-jaar periode substantieel te laten afwijken van 50 keer de faalkans per jaar. Dit is het geval wanneer onzekerheid over de (door de jaren heen gecorreleerde) sterkte domineert in de faalkans.
Het principe van het werken met langere referentieperioden dan één jaar is als volgt. De toelaatbare faalkans voor een langere referentieperiode wordt gegeven door vergelijking (A 1.31); dit is de faalkans eis voor de referentieperiode. Deze faalkans eis komt voort uit een beschouwing van aanvaardbare overstromingsrisico’s per jaar, die uit een (maatschappelijke) kosten/baten analyse volgen. Daarbij wordt geen rekening gehouden met het feit dat de feitelijke faalkansen door de jaren heen onderling afhankelijk kunnen zijn. Wanneer de feitelijke faalkansen per jaar door de jaren heen afhankelijk zijn, dan mogen de faalkansen per jaar groter zijn dan de toelaatbaar geachte faalkans per jaar die in vergelijking (A 1.31) is gebruikt. Er wordt dan toch nog voldaan aan de eis dat de feitelijke faalkans voor de langere referentieperiode kleiner is of gelijk aan de toelaatbare faalkans voor die referentieperiode. Daarmee wordt gebruik gemaakt van de boven beschreven interpretatie 2 van de beveiligingsnorm.
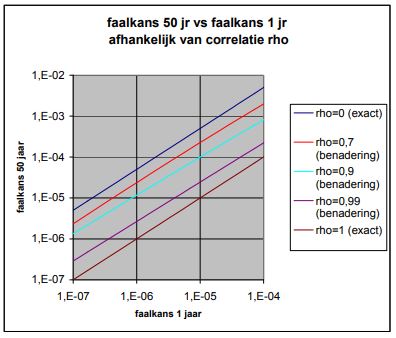
Figuur I.0.1 Relatie tussen feitelijke faalkansen, betrokken op één jaar, en hiermee overeenkomstige feitelijke faalkansen, betrokken op 50 jaar, als functie van de correlatiecoëfficiënt (rho).
Voordeel van toepassing langere referentieperiode
Het idee om afhankelijkheid van de feitelijke faalkansen per jaar in opeenvolgende jaren in de veiligheidsbeschouwing en veiligheidseisen te betrekken wordt al toegepast bij waterkerende kunstwerken. In de Leidraad Kunstwerken [TAW, 2003] is deze benadering vastgelegd, gebaseerd op de studie VeilKunWat (Veiligheidsfilosofie Kunstwerken in de natte Waterbouwkunde), die door Rijkswaterstaat in de jaren 1995-1997 is uitgevoerd. Deze leidraad is van toepassing op zowel harde waterkerende constructies als constructies waarin grondlichamen, die versterkt zijn met harde constructies (zoals damwanden, diepwanden, et cetera) het waterkerende vermogen leveren.
In de Leidraad Kunstwerken is als uitgangspunt gekozen voor een referentieperiode N=10 jaar. Dat betekent dat in probabilistische analyses om de feitelijke faalkans te toetsen uitgegaan mag worden van een faalkansruimte gelijk aan 10 keer faalkansruimte op jaarbasis.
Gevolg hiervan is dat probabilistische faalkans analyses, ten behoeve van het toetsen of ontwerpen van waterkeringen, gebaseerd worden op de volgende uitgangspunten:
a) De vereiste betrouwbaarheidsindex voor de referentieperiode van 10 jaar is kleiner dan de vereiste betrouwbaarheidsindex op jaarbasis. Bijvoorbeeld een vereiste betrouwbaarheidsindex van 4,80 op jaarbasis leidt tot een vereiste betrouwbaarheidsindex van 4,30 voor een referentieperiode van 10 jaar;
b) faalkansen voor de opvolgende jaren binnen de periode van 10 jaar worden berekend, op basis van de hydraulische belastingstatistiek en de karakterisering van (onzekerheid) van sterktevariabelen in elk van de 10 opvolgende jaren;
c) de faalkans in 10 jaar wordt samengesteld op basis van de berekende ‘jaar’ faalkansen, rekening houdend met afhankelijkheden. Afhankelijkheden worden berekend via correlaties van de betrouwbaarheidsfuncties in de opvolgende jaren. Stochastische variabelen (zowel aan de belasting- als aan de sterktekant) leveren een bijdrage aan de correlaties, wanneer correlatiecoëfficiënten van die stochastische variabelen in verschillende jaren gedurende de periode van 10 jaar ongelijk nul zijn. Het samenstellen van de faalkans in 10 jaar op basis van de faalkansen per jaar kan bijvoorbeeld met behulp van de Rackwitz-Hohenbichler methode.
Dit is de theoretische (algemene) benadering. In de praktijk zullen stochastische variabelen (zowel aan de belasting als sterktekant) óf in de verschillende jaren onafhankelijk gerealiseerd worden (correlatiecoëfficiënt = 0), óf gedurende de 10 jaren volledig gecorreleerd zijn (correlatiecoëfficiënt = 1). Wanneer vervolgens in elk van de 10 jaren de kansverdelingen van deze stochastische variabelen identiek zijn, kan de algemene benadering aanzienlijk vereenvoudigd worden. Het berekenen van de faalkansen voor de opvolgende 10 jaren wordt vervangen door één berekening van de faalkans voor de gehele periode van 10 jaar. Daarmee vervalt het samenstellen van de faalkans in 10 jaar op basis van de faalkansen per jaar, zoals genoemd onder punt c) boven. Uitgangspunten bij de berekening zijn:
a) de targetwaarde voor de betrouwbaarheidsindex blijft, ongewijzigd, die voor 10 jaar;
b) de (samengestelde) kansverdelingfunctie van de (volledig) gecorreleerde stochastische variabelen gedurende 10 jaar is gelijk aan de kansverdeling voor één jaar;
c) uit de kansverdeling van (volledig) ongecorreleerde stochastische variabelen voor één jaar wordt die voor een periode van 10 jaar afgeleid. Voor de hydraulische belastingen moeten we dus overgaan op een belastingstatistiek voor de referentieperiode van 10 jaar; deze is gemakkelijk af te leiden uit de belastingstatistiek voor de referentieperiode van één jaar.
d) De uitkomst van de probabilistische faalkans analyse is de faalkans in 10 jaar.
Bij een semi-probabilistische benadering, gebaseerd op deze laatste aannamen, heeft dit de volgende effecten:
- omdat de targetwaarde voor de betrouwbaarheidsindex voor de 10-jaar referentieperiode kleiner is, zullen vereiste veiligheidsfactoren op de sterktevariabelen kleiner dan bij beschouwing van een referentieperiode van één jaar;
-
bij een referentieperiode van 10 jaar zal de vereiste veiligheidsfactor op de belasting groter zijn dan bij een referentieperiode van één jaar.
De twee effecten zijn tegengesteld, maar netto leidt dit tot een iets minder streng ontwerp- en toetscriterium.
In het huidige toetsinstrumentarium voor gedetailleerde toetsing van dijken is de strikte interpretatie als uitgangspunt gekozen. Bij het ontwikkelen van nieuw instrumentarium binnen het project Toets- en Ontwerpinstrumentarium (TOI) moet worden afgewogen of het overgaan op een referentieperiode langer dan één jaar, structureel als uitgangspunt voor de gedetailleerde toetsing wordt gekozen. Hierop willen we niet vooruitlopen.
Voorgesteld wordt daarom voor de reguliere gedetailleerde toetsing de oude systematiek aan te houden en de toepassing van een langere referentieperiode (van 10 jaar) vooralsnog voor te behouden voor geavanceerde toetsingen.
