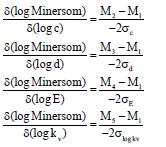Golfklap (AGK) - Toetsing

De nadruk voor de geavanceerde analyse zal in het algemeen liggen bij gegevensverzameling, waarbij ook geavanceerde meetmethodes kunnen worden gebruikt.

Als de geavanceerde analyse voortkomt uit het feit dat met GOLFKLAP in de gedetailleerde toetsing niet kan worden aangetoond dat de aanwezige laagdikte volstaat, kan overwogen worden om meer gegevens in te winnen. Hierbij kunnen ook geavanceerde meetmethodes worden gebruikt. De belangrijkste parameters zijn dan de sterkte (vermoeiingssterkte en breuksterkte), de stijfheid en de laagdikte van de bovenlaag en de beddingsconstante van de ondergrond. Ook een faalkansanalyse kan dan onderdeel uitmaken van een geavanceerde toetsing. Bij een faalkansanalyse wordt op basis van de spreiding in de relevante materiaalparameters een overschrijdingskans van de Minersom bij een gegeven belastingniveau bepaald. Een voorbeeld van een uitgevoerde faalkansanalyse is in deze paragraaf uitgewerkt.

Als de geavanceerde analyse wordt bereikt als gevolg van geconstateerde aantasting van het oppervlak (eenvoudige toets) ligt het voor de hand om de aantasting van het oppervlak nader te bestuderen. Het onderzoek van de aantasting heeft ten doel de eigenschappen van het bekledingsmateriaal ter plaatse van de aantasting te bepalen. Op basis van deze actuele bepaling van het mechanisch materiaalgedrag (de eigenschappen) op een bepaalde aangetaste locatie is de bekleding op het meest nauwkeurig te beoordelen op Golfklap. Het onderzoek kan ook informatie opleveren over de oorzaak van de geconstateerde aantasting. De oorzaak van de aantasting is een relevant gegeven, omdat er een verschil tussen de verwachte en aangetroffen situatie is.

Als de geavanceerde analyse wordt bereikt als gevolg van te hoge golfrandvoorwaarden (eenvoudige toets), dan dienen ook andere mogelijke faalmechanismen als gevolg van golfaanval te worden onderzocht. Om verweking van de ondergrond als gevolg van

golfklappen uit te kunnen sluiten, zullen de verdichtingsgraad van het dijklichaam en de ligging van de freatische lijn bepalend zijn.

Bij een gunstig resultaat is de deelscore voor Golfklap ‘voldoet’. Voorbeeld faalkansanalyse met GOLFKLAP

Om meer inzicht te krijgen in de overschrijdingskans van de berekende Minersom kan een

faalkansanalyse worden uitgevoerd. Deze analyse geeft inzicht op basis van de spreiding van de materiaalparameters. Als de karakteristieke waarden van de laagdikte, de beddingsconstante, de elasticiteitsmodulus en de breuksterkte bekend zijn, kan de kans berekend worden dat de Minersom groter is dan 1. Grote spreiding in de materiaalparameters leidt tot een grote onzekerheid in de Minersom.

Een voorbeeld van een faalkansanalyse wordt hier gegeven. In het jaar 2005 is een toetsing uitgevoerd op een oude asfaltbekleding. Uit de gedetailleerde beoordeling bleek dat de bekleding afgekeurd zou worden, er werd een Minersom groter dan 5 berekend. Om vast te stellen wat de overschrijdingskans van deze Minersom was, is een faalkansanalyse uitgevoerd.

De faalkansanalyse bestaat uit een probabilistische berekening die de Niveau 2 klasse 1 berekening wordt genoemd [94]. Om inzicht te krijgen in de veiligheidsmarges in de dijkbeoordelingsprocedure, kunnen een viertal probabilistische berekeningen worden uitgevoerd:

• Niveau I berekening: Dit is de deterministische berekening op basis van karakteristieke waarden zoals die nu wordt toegepast;

• Niveau II klasse 1 berekening: Deze berekening staat ook wel bekend als de “gemiddelde waarde berekening”. Deze berekening leidt onder strikte voorwaarden tot een exact resultaat. Aangezien vrijwel nooit aan deze strikte voorwaarden voldaan wordt, kan eventueel met behulp van een niveau III berekening worden nagegaan in hoeverre deze niveau II klasse 1 berekening een goede benadering is;

• Niveau II klasse 2 berekening: Deze berekening staat ook wel bekend als de “ontwerppunt berekening”. Deze berekening lijkt zeer sterk op de Niveau II klasse 1 berekening. Echter door de variatieberekeningen niet rond de gemiddelde waarde, maar rond het punt met de grootste kansbijdrage te maken, is de klasse 2 berekening nauwkeuriger wanneer niet aan de strikte voorwaarden wordt voldaan;

• Niveau III berekening: Deze berekening is een exacte berekening. Bij deze berekening wordt alle beschikbare data individueel beschouwd. Voor iedere set aan data wordt een berekening gemaakt, waardoor de verdeling van het resultaat van deze berekeningen exact is.

  De gedetailleerde beoordeling is in feite een Niveau I berekening. Nadeel is dat deze berekening geen inzicht geeft in faalkansen. De Niveau III berekening is zeer tijdrovend. Daar staat tegenover dat deze berekening een exacte verdeling van de faalkans geeft.

  De beide Niveau II berekeningen vergen ten opzichte van de Niveau I berekening slechts weinig extra rekenwerk en geven naar verwachting een zeer goede indruk in de faalkans. Gebleken is dat het verschil tussen de niveau II, klasse 1 berekening en de niveau III berekening gering zijn.

  Met een Niveau II berekening is het mogelijk om met weinig moeite een betrouwbaar beeld van de verdeling van de Minersom over een dijkvak te verkrijgen. Een Niveau II berekening geeft een exact resultaat wanneer wordt voldaan aan de volgende voorwaarden:

  i

  i

• M const dat wil zeggen alle verbanden zijn lineair en dus zijn alle afgeleiden constant.

  xi

• Er is geen covariantie, dat wil zeggen de variabelen hebben geen onderlinge afhankelijkheid.

• Alle verdelingen zijn normale verdelingen.

  Waarbij:

  M = Minersom

  xi = Verklarende variabelen, in het voorliggende geval stijfheid, laagdikte, beddingsconstante en breuksterkte

  Opmerking:

  Er zal wel een beperkte afhankelijkheid zijn. Een verandering van de stijfheid zal over het algemeen ook gepaard gaan met een verandering van vermoeiingseigenschappen. Een verandering van de laagdikte zal ook een verandering van de stijfheid tot gevolg hebben.

  Uit de radarmetingen en de valgewicht-deflectiemetingen zijn gemiddelde waarden (µ), respectievelijk standaardafwijking (a) gevonden voor log beddingsconstante (log c), laagdikte (d) en log stijfheid (log E). Het gemiddelde en de standaarddeviatie van de breuksterkte (abreuk) zijn ontleend aan de laboratoriumproeven.

  Er zijn per vak vijf berekeningen van de Minersom gemaakt met GOLFKLAP 1.3. Hierbij zijn de invoerparameters log(c), d, log(E) en log(kv) gevarieerd. Elke berekening levert een Minersom (M1...5) op. De eerste berekening wordt uitgevoerd met de gemiddelde waarden van log(c), d, log(E) en log(kv). Deze Minersom (M1) is de gemiddelde waarde van de verdeling van de Minersom. De standaardafwijking van de verdeling wordt berekend door met de waarden van log(c), d, log(E) en log(kv) te variëren door tweemaal de standaard- afwijking bij de gemiddelde waarde op te tellen of af te trekken.

  Vervolgens zijn benaderingen voor de afgeleiden van log Minersom naar log (c), d, log (E) en log(kv) bepaald:

  

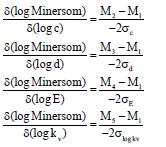
  Het gemiddelde en de standaarddeviatie van de log Minersom zijn bepaald met de volgende vergelijkingen:

  µlog minersom = M1

  Het resultaat is een lognormale verdeling van de Minersom waaruit de overschrijdingskans van de Minersom berekend kan worden. De berekende verdeling is weergegeven in onderstaande afbeelding.

  

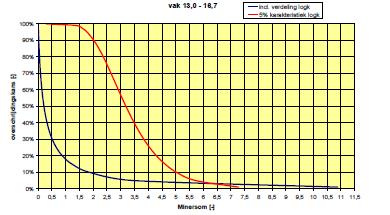
  Figuur 6-6: Berekende overschrijdingskans van de Minersom

  

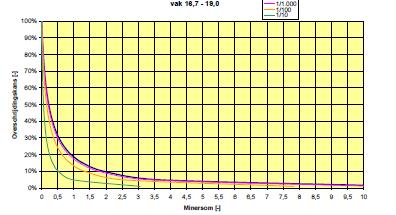
  Figuur 6-7: Overschrijdingskans van de Minersom bij verschillende hydraulische randvoorwaarden

  Het resultaat van de berekening is een overschrijdingskans van de Minersom van 18%. Dit is de overschrijdingskans van de Minersom bij de hydraulische randvoorwaarden zoals gebruikt in de gedetailleerde beoordeling. Uitgaande van de overbelastingsbenadering kan voor bekledingen worden gesteld dat - gegeven het optreden van de maatgevende randvoorwaarden - een faalkans kleiner dan 1% acceptabel is, terwijl een faalkans groter dan 10% onvoldoende veiligheid biedt. Door met hydraulische randvoorwaarden te rekenen met verschillende kansen van voor komen, kan inzicht verkregen worden in de over-

  schrijdingskans bij verschillende hydraulische randvoorwaarden. Dit is weergegeven in onderstaande afbeelding.

  Het bovenstaande voorbeeld van een geavanceerd beoordeling, een faalkansanalyse, biedt gegevens op basis waarvan de beslissing kan worden genomen om de bekleding te repareren of te reconstrueren.