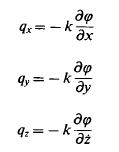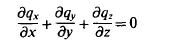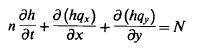Berekeningsmodellen - Waterspanningen en styghoogten

1. 1. 1. Algemeen

         Aan alle berekeningsmodellen liggen 2 principes ten grondslag:

         1. De wet van Darcy

            Voor homogene, onsamendrukbare vloeistof en isotrope doorlatendheid luidt deze:

            

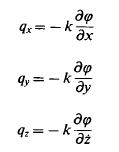
            met:

            q = specifiek debiet [m/s]

            k = doorlatendheidscoefficient [m/s]

            <p= z+ u/Qg= stijghoogte [m]

            z = plaatshoogte [m]

            ]

            u = waterspanning [N/m2

            ]

            (} = volumieke massa van water [kg/m3

            g = versnelling van de zwaartekracht [m/s2]

         2. De wet van behoud van massa

            Bij (quasi-)stationaire stroming volgt hieruit de zogenaamde continulteitsvergelij­ king:

            

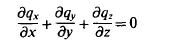
            Bij niet-stationaire stroming luidt deze continui teitsvergelijking als volgt:

            1. voor freatische berging:

         

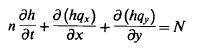
         met h = rp =de stijghoogte ten opzichte van de basis van het doorstroomde pak­ ket, N kan de hoeveelheid neerslag zijn, en n is de porositeit van de grond.

         b. voor elastische berging:

         

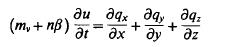
         Hierin staan mv en P· voor de samendrukbaarheid van de grond respectievelij k het water (par. 10.1.1). Deze vergelijking wordt ook we! aangeduid als bergingsverge­ lijking.

         Uit de wet van Darcy en de wet van behotid van massa volgt na samenstelling van de vergelijkingen de differentiaalvergelijking die de stroming beschrijft, uitgedrukt in <p of u.

         Uit het oplossen van deze vergelijking bij de van toepassing zijnde randvoorwaarden

         volgt het gezochte stromingsbeeld.

         Voor het oplossen zijn vier mogelijkheden beschikbaar:

         • een analytische oplossing,

         • een numerieke benadering,

         • een analoog model,

         • een grafische benadering.

         Op deze mogelijke oplossingmethoden wordt in de volgende paragrafen nader inge­ gaan. Maar eerst nog een opmerking over de schematisering van de werkelijkheid in een rekenmodel.

         De mate waarin de uitkomst van een berekening overeenkomt met de realiteit is sterk

         afhankelijk van het toegepaste rekenmodel, de schematisering en de nauwkeurigheid van de parameters die in de berekening een rol spelen.

         De grondwaterstroming is in principe een drie-dimensionaal verschijnsel. In die geval­

         len waarbij in een richting geen grote wijzigingen optreden in geometrie, grondparame­ ters en randvoorwaarden, is een schematisering tot twee dimensies mogelijk. De wijze waarop men schematiseert is echter ook afhankelijk van het beschouwde probleem. Twee-dimensionale horizontale schematisering zal in het algemeen worden toegepast bij het oplossen van regionale problemen.

         Twee-dimensionale verticale schematisering zal veelal worden toegepast bij de oplos­ sing van detailgerichte problemen.

         Bij het oplossen van grondwaterstromingsproblemen in relatie tot rivierdijkontwerpen zal in vrijwel alle gevallen een twee-dimensionale schematisering worden toegepast, aangezien drie-dimensionale berekeningen analytisch slecht uitvoerbaar zijn, en nu­ meriek nog erg kostbaar.

         Bovendien is het zeer de vraag of de uitkomsten van drie dimensionale berekeningen,

         enkele specifieke uitzonderingen daargelaten, de realiteit beter benaderen dan die van twee-dimensionale berekeningen, gelet op de onzekerheden die in de berekening wor­ den gelntroduceerd door de vaak sterke schematisering van de geometrie, en door de vaak slechts bij benadering bekende waarden van bepalende parameters.

         109

      2. Analytische model/en

         Dikwij Is kan men door toepassing van eenvoudige analytische modellen een redelijk in­ zicht verkrijgen in de grondwaterbeweging.

         Voorwaarde is wel, dat het mogelijk moet zijn de differentiaalvergelijking die de stro­ ming beschrijft, bij de gegeven randvoorwaarden langs analytische weg op te lossen. Een nadeel van de analytische oplossing is daaram dater dikwij ls een sterke schematisering van de geometrie van de te onderzoeken situatie nodig is, om tot een oplossing te komen. Het grate voordeel van het analytische model ligt vooral in het kwalitatieve inzicht dat dit model verschaft in het gedrag van de straming, en de invloed van de diverse parame­ ters daarap.

         In de appendices B en C warden enkele veel voorkomende gevallen gegeven, waarvan de analytische oplossing bekend is en die zo eenvoudig zijn dat zij een snelle schatting van het grandwaterstramingsbeeld mogelijk maken.

         Appendix B beschrijft in het bijzonder de volgende gevallen van stationaire straming:

         1. straming door een afdekkende laag;

         1. straming in een zandondergrand onder een ondoorlatende dijk, met slecht doorla­ tende, afdekkende lagen in het voor- en achterland, zonder radiate intree of uittree van water;

         2. straming in een zandondergrand onder een ondoorlatende dijk, met ondoorlatende

            lagen in het voor- en achterland, en met radiate intree en uittree van water;

         3. straming in een zandondergrand onder een ondoorlatende dijk en berm, waarbij binnendijks een grenspotentiaal optreedt.

         Appendix C geeft een benadering voor de niet-stationaire straming bij voortplanting van waterspanningen in een kleilaag met elastische berging.

      3. Numerieke model/en

De grate be perking van analytische mode lien ligt, zoals gezegd in de sterke schematise­ ring die daarbij vaak nodig is.

Dit nadeel geldt bij numerieke berekeningsmodellen veel minder, omdat hiermee in

principe oak meerlagensystemen, en dijkprafielen die uit verschillende grandsoorten

-------

zijn samengesteld, kunnen warden berekend, zowel stationair als niet-stationair.

Daar drie-dimensionale modellen erg veel rekentijd en een grate geheugencapaciteit van de computer vragen zijn de meeste berekeningsmodellen ontwikkeld voor twee­ dimensionale stramingsgevallen in het horizontale of het verticale vlak.

Mogelijke numerieke rekenmethoden zijn:

• eindige differentiemethode, expliciet of impliciet;

• eindige elementenmethode;

• analytische functiemethode. I IO

  Voor meer informatie hierover wordt verwezen naar de literatuur (lit. 37) en naar de programmadocumentatie van bestaande programma's.

  Vanwege de snelle ontwikkeling op het gebied van de numerieke rekenmodellen is het niet zinvol hier een overzicht van bestaande programma's met hun (on)mogelijkheden te geven.

  1. 1. 1. Analoge model/en

           Omdat de vergelijkingen die de beweging van het grondwater beschrijven in veel geval­ len analoog zijn aan de vergelijkingen voor andere fysische verschijnselen, zoals warmtegeleiding en geleiding van elektrische stroom, kan men oplossingen van grond­ waterstromingsproblemen vaak gemakkelijk verkrijgen met behulp van een zoge­ naamd analogon.

           De belangrijkste analoge methode voor de bestudering van grondwaterbewegingen is die van de elektrische analogie (zie ook lit. 34 en 43).

           De elektrische analogie berust op de overeenkomst tussen de wet van Darcy en de wet van Ohm voor de geleiding van elektrische stroom.

           Omdat er ook behoud van elektrische lading is - de continuiteit -is de analogie met grondwaterstroming volledig.

           In praktische toepassingen kan men als elektrische geleider een vloeistof nemen of een vaste stof, in het bijzonder een speciaal type papier dat voorzien is van een geleidende koolstoflaag.

           Voor het oplossen van eenvoudige praktische problemen voldoet deze methode goed. Problemen die met dit model kunnen warden opgelost zijn met name:

           • twee-dimensionale stromingssituaties;

           • problemen met stationaire randvoorwaarden;

             . - problemen met tijdsafhankelijke randvoorwaarden, waarbij de freatische berging met behulp van condensatoren kan warden gesimuleerd.

             Het model kent we! een aantal beperkingen:

           • de afmetingen van het model zijn beperkt;

           • het papier is temperatuur- en vochtgevoelig;

           • het papier is niet geheel homogeen en isotroop;

           • het oplossen van problemen bij een meerlagensysteem is uitvoeringstechnisch niet goed mogelijk;

           • de hoogte van het doorstroomde pakket is niet eenvoudig te varieren;

           • elastische berging kan niet warden gesimuleerd.

             Een toepassing van de elektrische analogie met uitgebreidere mogelijkheden is die, waarbij gebruik wordt gemaakt van een weerstandsnetwerk. Verschillen in door­ latendheid kan men dan simuleren door verschillende weerstanden te gebruiken.

             111

             Verder kan men berging simuleren met behulp van condensatoren. Voor het oplos­ sen van gecompliceerde problemen is bij de Rijkswaterstaat het Elektrisch Netwerk Analogon (ELNAG) ontwikkeld. De ELNAG is geschikt voor het oplossen van zowel stationaire als niet-stationaire twee-dimensionale grondwaterstromingsproble­ men.

             Door het discretiseren zijn alle genoemde bezwaren tegen de papieren modellen onder­

             vangen. Maar ook aan de ELNAG zijn nadelen verbonden: het is erg bewerkelijk en de capaciteit van het analogon wordt beperkt door het maximale aantal knooppunten (5000). Analoge modellen warden overigens steeds minder gebruikt, vanwege de snelle ontwikkeling in de numerieke computermodellen.