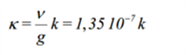- 1. Inleiding
- 2. Faalmechanisme piping
- Piping en interne erosie
- Faalpaden piping
- Initiërende gebeurtenis piping
- Fenomenologische beschrijving opdrijven en opbarsten
- Fenomenologische beschrijving heave
- Fenomenologische beschrijving terugschrijdende erosie
- Fenomenologische beschrijving vervolggebeurtenissen
- Samenvatting: wanneer kan terugschrijdende erosie optreden?
- 3. Modelleren van piping bij dijken
- 3.1 Modelleren van opdrijven en opbarsten
- 3.2 Modelleren heave
- 3.3 Modelleren terugschrijdende erosie
- Rekenmodellen terugschrijdende erosie
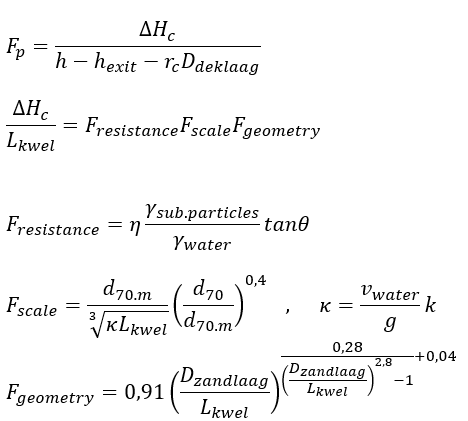
- Rekenregel van Sellmeijer
- Achtergrond rekenmodel van Sellmeijer
- Eindige elementen model D-GeoFlow
- Omgang met pipegroei onder voorland D-GeoFlow
- Drukval in een wel (0,3D-regel) bij terugschrijdende erosie
- Effecten tijdsafhankelijke buitenwaterstand op terugschrijdende erosie
- 4. Analyse geohydrologische situatie en belastingen
- 4.1 Geohydrologie rond de dijk
- 4.1.1 Inleiding geohydrologische analyses t.b.v. piping
- 4.1.2 Basisbegrippen
- Basisbegrippen waterspanningen
- Freatisch vlak en capillaire zone
- Freatische en elastische waterberging in grond
- Stijghoogte en potentiaal in het watervoerend pakket
- Grenspotentiaal en opdrijven
- Intreepunt
- Kantelpunt
- Lekfactor of leklengte
- Hydrodynamische periode
- Naijlen van waterspanningen
- Indringingslaag
- Responsfactor
- 4.1.3 Berekenen van waterspanningen
- 4.1.4 Grenspotentiaal in watervoerend pakket
- 4.2 Schematiseren en modelleren van de geohydrologische situatie
- 4.2.1 Schematiseren geohydrologische situatie
- 4.2.2 Omgaan met onzekerheden in een geohydrologisch model
- 4.2.3 Analytische modellen
- Modellen van het stijghoogteverloop in een zandlaag onder een ondoorlatende dijk
- Model van stationaire stroming onder dijk met deklaag op watervoerende laag in voor- en achterland (Model 4A)
- Model van stationaire stroming onder dijk gelegen op watervoerende laag (Model 4B)
- Model van stationaire stroming onder dijk met binnendijks de grenspotentiaal (Model 4C)
- Model voor stroming onder dijk, de respons op een sinusvormige hoogwatergolf (Model 4D)
- Model voor stroming onder de dijk, de respons op sinusvormige hoogwatergolven (Model 4E en 4F)
- Berekenen van de opdruklengte bij stationaire stroming (Model 3D)
- Rekenvoorbeeld van de opdruklengte bij stationaire stroming
- Berekenen van de opdruklengte bij niet-stationaire stroming
- Rekenvoorbeeld van de opdruklengte bij niet-stationaire stroming
- 4.2.4 Numerieke modellen
- 4.3 Meten van waterspanningen en stijghoogte
- Waterspanningen meten en/of monitoren
- Geohydrologie bij de dijk monitoren
- Bewaken ontwerpuitgangspunten waterspanningen
- Instrumenten om waterspanningen te meten
- Valkuilen bij interpreteren van waterspanningsmetingen
- Voorbeeld van valkuilen bij interpreteren van waterspanningsmetingen
- Analytische modellen voor de interpretatie van peilbuiswaarnemingen
- Interpretatie gemeten stijghoogteverloop voor cyclische belasting (Model 3B)
- Niet-stationaire benadering met behulp van de transiënte lekfactor (Model 3C)
- Interpretatie van peilbuiswaarnemingen bij het onderstromen van hoog voorland
- 4.4 Gebruik van een geohydrologisch model in de analyse van piping
- 4.1 Geohydrologie rond de dijk
- 5. Karakteriseren eigenschappen van het watervoerend pakket
- 6. Veiligheidsanalyse piping
- 7. Oplossingen voor dijkverbeteringen
Rekenregel van Sellmeijer
Literatuur
De Vries, G. SBW Hervalidatie Piping : HP5.4a Inrichting en aanleg full-scale experiment. Deltares, rapport 1200960-000-GEO-0021, september 2009.
Förster, U., G. van den Ham, E. Calle en G. Kruse. Onderzoeksrapport zandmeevoerende wellen. Deltares, rapport 1202123-003-GEO-0002, maart 2012.
Koelewijn, A.R. SBW Hervalidatie piping E. Evaluatie 0,3d rekenregel. Deltares, rapport 1001453-002- GE0-0001, april 2009.
Knoeff, J.G., J. Lopez de la Cruz, J.B. Sellmeijer, S. Luijendijk en V.M. van Beek. SBW Piping - Hervalidatie piping : HP1 Ontwikkeling nieuwe rekenregel, HP1.2 Uitbreiding en aanpassing van de pipingregel. Deltares, rapport 1200187-015-GEO-0004, oktober 2009.
Sellmeijer, J.B. On the mechanism of piping under impervious structures. Technische Universiteit Delft, doctoral thesis, 1988.
Schematiseringshandleiding piping ; Versie 4.0 definitief ; WBI 2017. Rijkswaterstaat (RWS WVL), mei 2021.
Sellmeijer, J.B., J.L. de la Cruz, V. van Beek en H. Knoeff. Fine-tuning of the backward erosion piping model through small-scale, medium-scale and IJkdijk experiments. European Journal of Environmental and Civil Engineering 15(8), 1139-1154, 2011.
Van Beek, V., R. Hoogendoorn, E. Rosenbrand, M.P. Hijma. Kennis voor Keringen : Syntheserapport pipingonderzoek 2018-2019. Deltares, rapport 11203719-019-GEO-0003, maart 2020.
Van Beek, V. Use of the 0.3D rule in D-Geo Flow Deltares rapport 11200575-028-GEO-0003, maart 2019.