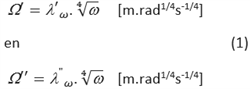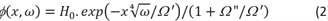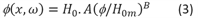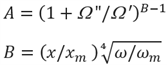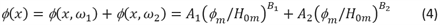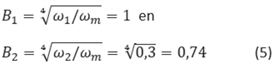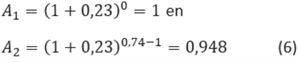- 1. Inleiding
- 2. Faalmechanisme piping
- Piping en interne erosie
- Faalpaden piping
- Initiërende gebeurtenis piping
- Fenomenologische beschrijving opdrijven en opbarsten
- Fenomenologische beschrijving heave
- Fenomenologische beschrijving terugschrijdende erosie
- Fenomenologische beschrijving vervolggebeurtenissen
- Samenvatting: wanneer kan terugschrijdende erosie optreden?
- 3. Modelleren van piping bij dijken
- 3.1 Modelleren van opdrijven en opbarsten
- 3.2 Modelleren heave
- 3.3 Modelleren terugschrijdende erosie
- Rekenmodellen terugschrijdende erosie
- Rekenregel van Sellmeijer
- Achtergrond rekenmodel van Sellmeijer
- Eindige elementen model D-GeoFlow
- Omgang met pipegroei onder voorland D-GeoFlow
- Drukval in een wel (0,3D-regel) bij terugschrijdende erosie
- Effecten tijdsafhankelijke buitenwaterstand op terugschrijdende erosie
- 4. Analyse geohydrologische situatie en belastingen
- 4.1 Geohydrologie rond de dijk
- 4.1.1 Inleiding geohydrologische analyses t.b.v. piping
- 4.1.2 Basisbegrippen
- Basisbegrippen waterspanningen
- Freatisch vlak en capillaire zone
- Freatische en elastische waterberging in grond
- Stijghoogte en potentiaal in het watervoerend pakket
- Grenspotentiaal en opdrijven
- Intreepunt
- Kantelpunt
- Lekfactor of leklengte
- Hydrodynamische periode
- Naijlen van waterspanningen
- Indringingslaag
- Responsfactor
- 4.1.3 Berekenen van waterspanningen
- 4.1.4 Grenspotentiaal in watervoerend pakket
- 4.2 Schematiseren en modelleren van de geohydrologische situatie
- 4.2.1 Schematiseren geohydrologische situatie
- 4.2.2 Omgaan met onzekerheden in een geohydrologisch model
- 4.2.3 Analytische modellen
- Modellen van het stijghoogteverloop in een zandlaag onder een ondoorlatende dijk
- Model van stationaire stroming onder dijk met deklaag op watervoerende laag in voor- en achterland (Model 4A)
- Model van stationaire stroming onder dijk gelegen op watervoerende laag (Model 4B)
- Model van stationaire stroming onder dijk met binnendijks de grenspotentiaal (Model 4C)
- Model voor stroming onder dijk, de respons op een sinusvormige hoogwatergolf (Model 4D)
- Model voor stroming onder de dijk, de respons op sinusvormige hoogwatergolven (Model 4E en 4F)
- Berekenen van de opdruklengte bij stationaire stroming (Model 3D)
- Rekenvoorbeeld van de opdruklengte bij stationaire stroming
- Berekenen van de opdruklengte bij niet-stationaire stroming
- Rekenvoorbeeld van de opdruklengte bij niet-stationaire stroming
- 4.2.4 Numerieke modellen
- 4.3 Meten van waterspanningen en stijghoogte
- Waterspanningen meten en/of monitoren
- Geohydrologie bij de dijk monitoren
- Bewaken ontwerpuitgangspunten waterspanningen
- Instrumenten om waterspanningen te meten
- Valkuilen bij interpreteren van waterspanningsmetingen
- Voorbeeld van valkuilen bij interpreteren van waterspanningsmetingen
- Analytische modellen voor de interpretatie van peilbuiswaarnemingen
- Interpretatie gemeten stijghoogteverloop voor cyclische belasting (Model 3B)
- Niet-stationaire benadering met behulp van de transiënte lekfactor (Model 3C)
- Interpretatie van peilbuiswaarnemingen bij het onderstromen van hoog voorland
- 4.4 Gebruik van een geohydrologisch model in de analyse van piping
- 4.1 Geohydrologie rond de dijk
- 5. Karakteriseren eigenschappen van het watervoerend pakket
- 6. Veiligheidsanalyse piping
- 7. Oplossingen voor dijkverbeteringen
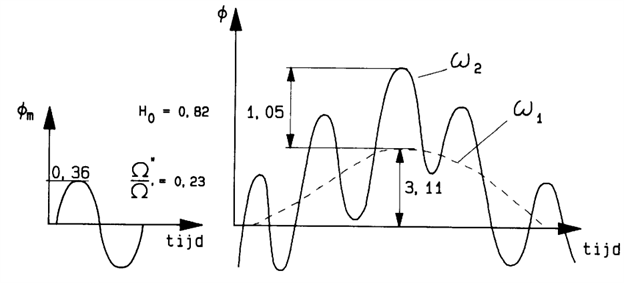
Model voor stroming onder de dijk, de respons op sinusvormige hoogwatergolven (Model 4E en 4F)
Gerelateerde artikelen
- Modellen van het stijghoogteverloop in een zandlaag onder een ondoorlatende dijk
- Model van stationaire stroming onder dijk met deklaag op watervoerende laag in voor- en achterland (Model 4A)
- Model van stationaire stroming onder dijk gelegen op watervoerende laag (Model 4B)
- Model van stationaire stroming onder dijk met binnendijks de grenspotentiaal (Model 4C)
- Model voor stroming onder dijk, de respons op een sinusvormige hoogwatergolf (Model 4D)
Literatuur
Bauduin, CHR, M.L.G. en F.B.J. Barends. Getijde respons in grondwater onder Nederlandse dijken H2O deel 21(1/88), p. 2-5, 1988.