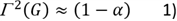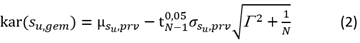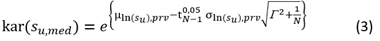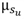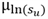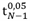- 1. Mechanismen geotechnische instabiliteit
- 1.1 Introductie
- 1.2 Instabiliteit in binnenwaartse richting
- Beschrijving afschuiven langs diep glijvlak binnenwaarts
- Vervolgmechanismen na binnenwaarts afschuiven langs diep glijvlak
- Kritisch glijvlak en vervolgmechanismen bij afschuiven langs diep glijvlak
- Controle van de binnenwaartse stabiliteit na een binnenwaartse afschuiving
- Afschuiven en/of afdrukken van de bekleding en uitspoelen
- Controle op uitspoelen na een binnenwaartse afschuiving
- Controle van erosie kruin en binnentalud na een binnenwaartse afschuiving
- Afschuiven langs een diep glijvlak bij opdrukken achterland
- Binnenwaarts afschuiven en drainagetechnieken
- 1.3 Afschuiven buitenwaarts en afschuiven voorland
- 2. Veiligheidsanalyse mechanisme afschuiven langs een glijvlak
- 2.1 Technieken voor de veiligheidsanalyse
- 2.2 Model- en veiligheidsfactoren
- Partiële veiligheidsfactoren voor geotechnische stabiliteit
- Materiaalfactor voor afschuiven langs diep glijvlak
- Modelfactor voor afschuiven langs diep glijvlak
- Schadefactor voor afschuiven langs diep glijvlak
- Schadefactor voor een constructief versterkte dijk (langsconstructie)
- Schematiseringfactor voor afschuiven
- Veiligheidsanalyse afschuiven en/of afdrukken van de bekleding en uitspoelen
- Voorbeeld schematiseringfactor voor afschuiven
- Rekenblok schematiseringfactor voor afschuiven diep glijvlak
- 3. Belastingen
- 3.1 Inleiding
- 3.2 Waterspanningen
- 3.2.1 Inleiding waterspanningen
- 3.2.2 Bepalen waterspanningen
- Grondwaterstroming algemeen
- Waterspanningen meten en/of monitoren
- Geohydrologie bij de dijk monitoren
- Bewaken ontwerpuitgangspunten waterspanningen
- Instrumenten om waterspanningen te meten
- Valkuilen bij interpreteren van waterspanningsmetingen
- Voorbeeld van valkuilen bij interpreteren van waterspanningsmetingen
- Schematiseren van de waterspanningen
- Schematiseren waterspanningen stap 1: Beschrijving bodemopbouw, grondwaterstroming en geometrie
- Schematiseren waterspanningen stap 2: Mechanismen en belastingcombinaties
- Schematiseren waterspanningen stap 3: Modelkeuze, schematisering en verificatie
- Onzekerheid waterspanningsschematisering
- Eerste schatting van waterspanningen
- Analytische modellen voor de interpretatie van peilbuiswaarnemingen
- Interpretatie gemeten stijghoogteverloop voor cyclische belasting (Model 3B)
- Niet-stationaire benadering met behulp van de transiënte lekfactor (Model 3C)
- Interpretatie van peilbuiswaarnemingen bij het onderstromen van hoog voorland
- Berekenen waterspanningen
- Theorie achter het berekenen van waterspanningen
- Rekenprogramma's grondwaterstroming
- 3.2.3 Freatisch vlak in de dijk
- Ligging freatisch vlak in de dijk
- Eerste schatting van het freatisch vlak
- Rekenregel voor bepalen van de hoogte freatisch vlak in kleidijk
- Infiltratie naar het freatisch vlak
- Invloed van golfoverslag op het freatisch vlak
- Invloed van neerslag op het freatisch vlak
- Freatisch vlak na snelle val buitenwaterstand: analytische oplossing
- 3.2.4 Stijghoogten in watervoerende laag
- Stijghoogten bepalen in het watervoerend pakket
- Eerste schatting van de stijghoogte in het watervoerend pakket (Model 3A)
- Schematiseren stijghoogteverloop in zandlaag na opdrukken
- Berekenen van de grenspotentiaal
- Modellen van het stijghoogteverloop in een zandlaag onder een ondoorlatende dijk
- Model van stationaire stroming onder dijk met deklaag op watervoerende laag in voor- en achterland (Model 4A)
- Model van stationaire stroming onder dijk gelegen op watervoerende laag (Model 4B)
- Model van stationaire stroming onder dijk met binnendijks de grenspotentiaal (Model 4C)
- Model voor stroming onder dijk, de respons op een sinusvormige hoogwatergolf (Model 4D)
- Model voor stroming onder de dijk, de respons op sinusvormige hoogwatergolven (Model 4E en 4F)
- Berekenen van de opdruklengte bij stationaire stroming (Model 3D)
- Rekenvoorbeeld van de opdruklengte bij stationaire stroming
- Berekenen van de opdruklengte bij niet-stationaire stroming
- Rekenvoorbeeld van de opdruklengte bij niet-stationaire stroming
- Waterspanningen voor buitenwaartse stabiliteit
- 3.3 Overige belastingen
- 4. Karakteriseren van dijklichaam en ondergrond
- 4.1 Externe geometrie
- 4.2 Ondergrond en grondlichaam
- Geologische beschrijving van de ondergrond
- Veen
- Bepalen van grondeigenschappen
- Basisopzet van grondonderzoek
- Strategie opzet grondonderzoek
- Gebruik van beschikbare informatie bij grondonderzoek
- Grondonderzoek van grof naar fijn
- Algemene aanbevelingen bij het gebruik van sonderingen voor parameterbepaling
- 4.3 Bodemopbouw
- 4.4 Schuifsterkte parameters
- Grondgedrag en rol van in situ toestand
- Schuifsterke in CSSM-model
- Keuze gedraineerd of ongedraineerd grondgedrag
- Gedraineerde schuifsterkte
- Cohesie van grond
- Hoek van inwendige wrijving
- Hoek van inwendige wrijving bepalen uit metingen
- Ongedraineerde schuifsterkte
- Normaal geconsolideerde ongedraineerde schuifsterkte ratio S
- Voorbeelden bepalen schuifsterkte ratio S
- Sterktetoename-exponent m
- Grensspanning, POP en OCR
- Grensspanning in het ontwerp
- Toename ongedraineerde schuifsterkte in de tijd
- Stapsgewijs bepalen ongedraineerde schuifsterkteparameters
- Ongedraineerde sterkte uit gebiedspecifieke correlaties met sonderingen
- Ongedraineerde schuifsterkte uit correlaties met sonderingen
- Ruimtelijke variabiliteit van de sondeerweerstand
- Su en POP bepalen uit één sondering
- Su en POP bepalen uit meerdere sonderingen
- Grensspanning, POP en OCR uit schuifsterkteparameters afgeleid uit sonderingen
- Ongedraineerde schuifsterkte van zware zandige siltige klei
- Schuifsterkte in de (initieel) onverzadigde zone
- Piek-schuifsterkte versus grote-rek-schuifsterkte
- Schuifsterkte bij ondiepe glijvlakken en afschuiven bekleding
- 4.5 Doorlatendheid
- 4.6 Vervormingseigenschappen
- 4.7 Overige grondparameters
- 4.8 Karakteristieke schattingen van grondparameters
- 5. Rekenmodellen voor geotechnische instabiliteit
- Rekenmodellen afschuiven
- Methode Bishop
- Methode LiftVan, rekenmodel afschuiven langs diep glijvlak
- Methode Spencer, rekenmodel afschuiven
- Glijvlak zoekroutines
- Rekenen aan afschuiven bij opdrukken achterland
- Rekenmodellen voor afschuiven en/of afdrukken van de bekleding en uitspoelen
- Rekenmodel afdrukken bekleding
- Rekenmodel uitspoelen en afschuiven van zand zonder kleibekleding
- Rekenmodel uitspoelen zand door bekleding
- 6. Oplossingen voor dijkverbetering
- 6.1 Uitvoering
- Uitvoering dijkverbetering
- Veiligheid waterkering tijdens dijkverbetering
- Stabiliteit tijdens de uitvoering dijkverbetering
- Uitvoeringsbegeleiding dijkverbetering
- Kwaliteitscontrole bij uitvoering dijkverbetering
- Koppeling tussen ontwerp en uitvoering van dijkverbetering
- Overhoogte bij uitvoering dijkverbetering
- Aanbrengen en verdichten van grond
- 6.1 Uitvoering
- 7. Beheer
Karakteristieke waarde op basis van een regionale proevenverzameling
Literatuur
Calle, E.O.F. en M.T. van der Meer. Probabilisme in de Geotechniek. (Studie i.o.v. Rijkswaterstaat DWW met diverse rapportages van GeoDelft en Fugro - Onderdeel Ruimtelijke variabiliteit, Fase AIII) Grondmechanica Delft, rapport CO-361410/95, Delft, december 1997.
TAW. Leidraadvoor het ontwerpen van rivierdijken deel 2 – benedenrivierengebied. TAW. ’s-Gravenhage, september 1989.
Esch, J.M. van. Statistische verwerking van cel- en triaxiaalproeven. Rapport GeoDelft, rapport SE-50676. Delft, februari 1997.