- 1. Mechanismen geotechnische instabiliteit
- 1.1 Introductie
- 1.2 Instabiliteit in binnenwaartse richting
- Beschrijving afschuiven langs diep glijvlak binnenwaarts
- Vervolgmechanismen na binnenwaarts afschuiven langs diep glijvlak
- Kritisch glijvlak en vervolgmechanismen bij afschuiven langs diep glijvlak
- Controle van de binnenwaartse stabiliteit na een binnenwaartse afschuiving
- Afschuiven en/of afdrukken van de bekleding en uitspoelen
- Controle op uitspoelen na een binnenwaartse afschuiving
- Controle van erosie kruin en binnentalud na een binnenwaartse afschuiving
- Afschuiven langs een diep glijvlak bij opdrukken achterland
- Binnenwaarts afschuiven en drainagetechnieken
- 1.3 Afschuiven buitenwaarts en afschuiven voorland
- 2. Veiligheidsanalyse mechanisme afschuiven langs een glijvlak
- 2.1 Technieken voor de veiligheidsanalyse
- 2.2 Model- en veiligheidsfactoren
- Partiële veiligheidsfactoren voor geotechnische stabiliteit
- Materiaalfactor voor afschuiven langs diep glijvlak
- Modelfactor voor afschuiven langs diep glijvlak
- Schadefactor voor afschuiven langs diep glijvlak
- Schadefactor voor een constructief versterkte dijk (langsconstructie)
- Schematiseringfactor voor afschuiven
- Veiligheidsanalyse afschuiven en/of afdrukken van de bekleding en uitspoelen
- Voorbeeld schematiseringfactor voor afschuiven
- Rekenblok schematiseringfactor voor afschuiven diep glijvlak
- 3. Belastingen
- 3.1 Inleiding
- 3.2 Waterspanningen
- 3.2.1 Inleiding waterspanningen
- 3.2.2 Bepalen waterspanningen
- Grondwaterstroming algemeen
- Waterspanningen meten en/of monitoren
- Geohydrologie bij de dijk monitoren
- Bewaken ontwerpuitgangspunten waterspanningen
- Instrumenten om waterspanningen te meten
- Valkuilen bij interpreteren van waterspanningsmetingen
- Voorbeeld van valkuilen bij interpreteren van waterspanningsmetingen
- Schematiseren van de waterspanningen
- Schematiseren waterspanningen stap 1: Beschrijving bodemopbouw, grondwaterstroming en geometrie
- Schematiseren waterspanningen stap 2: Mechanismen en belastingcombinaties
- Schematiseren waterspanningen stap 3: Modelkeuze, schematisering en verificatie
- Onzekerheid waterspanningsschematisering
- Eerste schatting van waterspanningen
- Analytische modellen voor de interpretatie van peilbuiswaarnemingen
- Interpretatie gemeten stijghoogteverloop voor cyclische belasting (Model 3B)
- Niet-stationaire benadering met behulp van de transiënte lekfactor (Model 3C)
- Interpretatie van peilbuiswaarnemingen bij het onderstromen van hoog voorland
- Berekenen waterspanningen
- Theorie achter het berekenen van waterspanningen
- Rekenprogramma's grondwaterstroming
- 3.2.3 Freatisch vlak in de dijk
- Ligging freatisch vlak in de dijk
- Eerste schatting van het freatisch vlak
- Rekenregel voor bepalen van de hoogte freatisch vlak in kleidijk
- Infiltratie naar het freatisch vlak
- Invloed van golfoverslag op het freatisch vlak
- Invloed van neerslag op het freatisch vlak
- Freatisch vlak na snelle val buitenwaterstand: analytische oplossing
- 3.2.4 Stijghoogten in watervoerende laag
- Stijghoogten bepalen in het watervoerend pakket
- Eerste schatting van de stijghoogte in het watervoerend pakket (Model 3A)
- Schematiseren stijghoogteverloop in zandlaag na opdrukken
- Berekenen van de grenspotentiaal
- Modellen van het stijghoogteverloop in een zandlaag onder een ondoorlatende dijk
- Model van stationaire stroming onder dijk met deklaag op watervoerende laag in voor- en achterland (Model 4A)
- Model van stationaire stroming onder dijk gelegen op watervoerende laag (Model 4B)
- Model van stationaire stroming onder dijk met binnendijks de grenspotentiaal (Model 4C)
- Model voor stroming onder dijk, de respons op een sinusvormige hoogwatergolf (Model 4D)
- Model voor stroming onder de dijk, de respons op sinusvormige hoogwatergolven (Model 4E en 4F)
- Berekenen van de opdruklengte bij stationaire stroming (Model 3D)
- Rekenvoorbeeld van de opdruklengte bij stationaire stroming
- Berekenen van de opdruklengte bij niet-stationaire stroming
- Rekenvoorbeeld van de opdruklengte bij niet-stationaire stroming
- Waterspanningen voor buitenwaartse stabiliteit
- 3.3 Overige belastingen
- 4. Karakteriseren van dijklichaam en ondergrond
- 4.1 Externe geometrie
- 4.2 Ondergrond en grondlichaam
- Geologische beschrijving van de ondergrond
- Veen
- Bepalen van grondeigenschappen
- Basisopzet van grondonderzoek
- Strategie opzet grondonderzoek
- Gebruik van beschikbare informatie bij grondonderzoek
- Grondonderzoek van grof naar fijn
- Algemene aanbevelingen bij het gebruik van sonderingen voor parameterbepaling
- 4.3 Bodemopbouw
- 4.4 Schuifsterkte parameters
- Grondgedrag en rol van in situ toestand
- Schuifsterke in CSSM-model
- Keuze gedraineerd of ongedraineerd grondgedrag
- Gedraineerde schuifsterkte
- Cohesie van grond
- Hoek van inwendige wrijving
- Hoek van inwendige wrijving bepalen uit metingen
- Ongedraineerde schuifsterkte
- Normaal geconsolideerde ongedraineerde schuifsterkte ratio S
- Voorbeelden bepalen schuifsterkte ratio S
- Sterktetoename-exponent m
- Grensspanning, POP en OCR
- Grensspanning in het ontwerp
- Toename ongedraineerde schuifsterkte in de tijd
- Stapsgewijs bepalen ongedraineerde schuifsterkteparameters
- Ongedraineerde sterkte uit gebiedspecifieke correlaties met sonderingen
- Ongedraineerde schuifsterkte uit correlaties met sonderingen
- Ruimtelijke variabiliteit van de sondeerweerstand
- Su en POP bepalen uit één sondering
- Su en POP bepalen uit meerdere sonderingen
- Grensspanning, POP en OCR uit schuifsterkteparameters afgeleid uit sonderingen
- Ongedraineerde schuifsterkte van zware zandige siltige klei
- Schuifsterkte in de (initieel) onverzadigde zone
- Piek-schuifsterkte versus grote-rek-schuifsterkte
- Schuifsterkte bij ondiepe glijvlakken en afschuiven bekleding
- 4.5 Doorlatendheid
- 4.6 Vervormingseigenschappen
- 4.7 Overige grondparameters
- 4.8 Karakteristieke schattingen van grondparameters
- 5. Rekenmodellen voor geotechnische instabiliteit
- Rekenmodellen afschuiven
- Methode Bishop
- Methode LiftVan, rekenmodel afschuiven langs diep glijvlak
- Methode Spencer, rekenmodel afschuiven
- Glijvlak zoekroutines
- Rekenen aan afschuiven bij opdrukken achterland
- Rekenmodellen voor afschuiven en/of afdrukken van de bekleding en uitspoelen
- Rekenmodel afdrukken bekleding
- Rekenmodel uitspoelen en afschuiven van zand zonder kleibekleding
- Rekenmodel uitspoelen zand door bekleding
- 6. Oplossingen voor dijkverbetering
- 6.1 Uitvoering
- Uitvoering dijkverbetering
- Veiligheid waterkering tijdens dijkverbetering
- Stabiliteit tijdens de uitvoering dijkverbetering
- Uitvoeringsbegeleiding dijkverbetering
- Kwaliteitscontrole bij uitvoering dijkverbetering
- Koppeling tussen ontwerp en uitvoering van dijkverbetering
- Overhoogte bij uitvoering dijkverbetering
- Aanbrengen en verdichten van grond
- 6.1 Uitvoering
- 7. Beheer
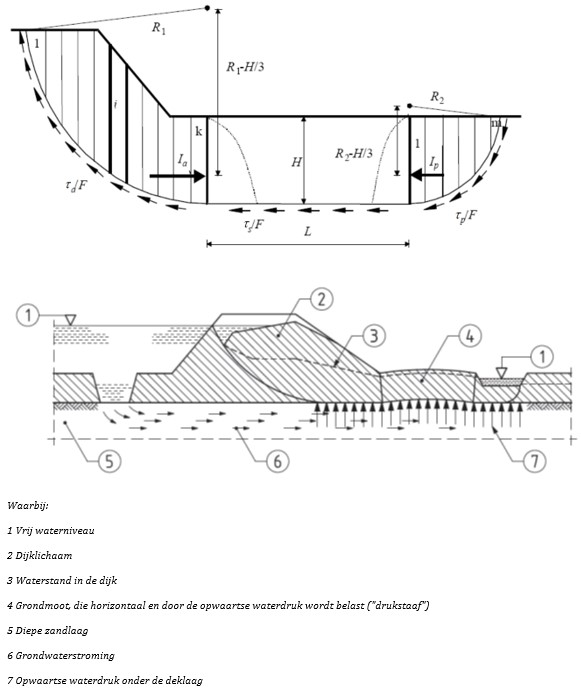
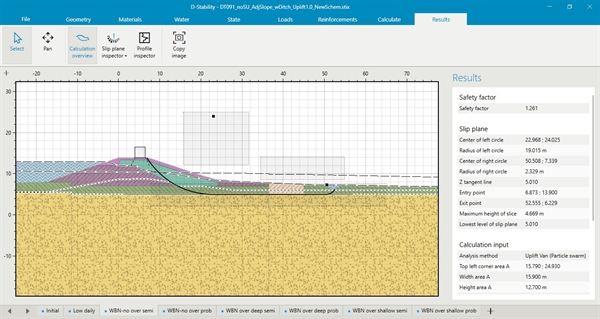
Methode LiftVan, rekenmodel afschuiven langs diep glijvlak
Gerelateerde artikelen
Literatuur
D-Stability op Deltares-website.
Van, M.A. A New Approach for Uplift induced Slope Failure ; in Proceedings 15th. International Conference on Soil Mechanics and Geotechnical Engineering, Istanbul 2001. Volume 3, pp. 2285-2288. Rotterdam, Balkema, 2001.