- 1. Mechanismen dijkerosie
- 1.1 Fenomenologische beschrijvingen
- Fenomenologische beschrijving van het mechanisme dijkerosie
- 1.1.1. Steenzettingen
- Fenomenologische beschrijving van de stabiliteit van een steenzetting op het buitentalud
- Falen van teen-, overgangs- of aansluitingsconstructie
- Bezwijkmechanismen van aan steenzettingen verwante bekledingstypen
- Bezwijken van ingegoten steenzettingen
- Bezwijken van geschakelde steenzettingen
- Bezwijken van doorgroeistenen
- Bezwijken van steenzetting op een berm
- Bezwijken steenzettingen door niet-hydraulische beschadiging
- 1.1.2 Asfaltbekledingen
- 1.1.3 Grasbekledingen
- Fenomenologische beschrijving van de grasbekleding op het buitentalud
- Fenomenologische beschrijving van de grasbekleding op de kruin en het binnentalud
- Uittrekmechanisme bij grasbekledingen
- Schade door stromingingsconcentraties langs objecten
- Schade door stroming rond niet goed beheerbare delen
- Slijterosie van grasbekledingen
- Erosie van overgangen / discontinuïteiten in grasbekledingen
- Jet-erosie bij grasbekledingen
- Afstropen van de grasbekleding
- Headcut erosie bij grasbekledingen
- 1.1.4 Breuksteenbekleding
- 1.2 Beschrijving dijkbekledingen
- 1.2.1 Steenzettingen
- Beschrijving van de verschillende onderdelen van een steenzetting
- Functies van een steenzetting
- Varianten in steenbekledingssystemen
- Toplaag steenzetting van standaardelementen
- Toplaag steenzetting van aanverwante bekledingstypen
- Ingezande en ingeslibte toplaag van de steenzetting
- Inwasmateriaal in een steenzetting
- Granulaire laag van een steenzetting
- Granulaire aanvulling van een dijklichaam onder een steenzetting
- Geokunststof in steenzettingen
- 1.2.2. Asfaltbekledingen
- 1.2.3 Grasbekledingen
- 1.2.4 Breuksteenconstructies
- 1.2.1 Steenzettingen
- 1.1 Fenomenologische beschrijvingen
- 2. Veiligheidsanalyse dijkerosie
- 3. Belastingen
- Hydraulische belastingen op dijkbekledingen
- Belastingzones voor zee- en estuariadijken
- 3.1 Waterstanden
- 3.2 Belastingverloop
- Belastingverloop bekledingen
- Waterstandsverloop voor het mechanisme toplaaginstabiliteit van zetsteen (ZST)
- Waterstandsverloop voor het mechanisme bezwijken van de asfaltbekleding (AGK en ASP)
- Waterstandsverloop voor het mechanisme erosie van de grasbekleding op het buitentalud (GEBU oploop en golfklap)
- Belastingduur voor het mechanisme erosie van de grasbekleding op de kruin en het binnentalud (GEKB)
- 3.3 Golven
- Bepaling van de golfhoogte gegeven een overschrijdingsfrequentie
- Golfcondities per waterstandsniveau
- Golfoverslag en overloop - definities
- Golfoploop
- Effect ruwheid steenzetting op golfoploop
- Golfklappen
- Gemiddeld overslagdebiet
- Vertaling van gemiddeld golfoverslagdebiet naar golfhoogte
- Simuleren hydraulische belasting voor afschuiven grasbekleding binnentalud
- Proeven met de golfoverslagsimulator
- Golfoverslag simuleren met een golfoverslagsimulator
- Stroomsnelheid en laagdikte op de kruin bij overslag
- Verloop snelheden tijdens overslag
- Aantal golven voor ontwerp en toetsing van breuksteen
- 3.4 Overige belastingen
- 4. Karakteriseren van dijklichaam en bekledingen
- 4.1 Dijkprofiel en voorland
- 4.2 Parameters steenzetting
- 4.2.1 Toplaagelementen
- Dikte toplaagelement steenzetting
- Het bepalen van de toplaagdikte van een steenzetting
- Dichtheid toplaagelement steenzetting
- Open ruimte tussen toplaagelementen steenzetting
- Open oppervlak toplaagelementen steenzetting
- De korrelgrootte van het inwasmateriaal van een toplaagelement steenzetting
- Parameters voor bepalen toplaaginstabiliteit door langsstroming
- Parameters voor bepalen toplaaginstabiliteit door golfoploop
- 4.2.2. Granulaire laag
- Eigenschappen granulaire laag
- Materiaaleigenschappen granulaire laag onder steenzettingen
- Het bepalen van representatieve parameters voor granulaire aanvullingen in steenzettingen
- Dikte van de granulaire laag onder steenzettingen
- (Conservatieve) Standaardwaarden voor de porositeit van de granulaire laag bij steenzettingen
- 4.2.3 Geokunststof en onderlagen
- 4.2.4. Overige invloedsparameters voor stabiliteit steenzettingen
- 4.2.1 Toplaagelementen
- 4.3 Parameters asfalt
- 4.3.1 Mechanische eigenschappen asfaltbekleding
- De laagdikte van een asfaltbekleding
- Stijfheid asfaltbekleding
- Valgewicht-deflectiemeter
- De doorlatendheid van asfalt
- Sterkte asfaltbekleding
- De holle ruimte van asfaltbekleding
- De dichtheid van asfaltbekleding
- De beddingsconstante van de ondergrond bij een asfaltbekleding
- De doorlatendheid van de ondergrond te beschouwen voor opdrijven gesloten bekleding
- 4.3.2 Testen voor eigenschappen asfaltbekleding
- Bepalen karakteristieke waarden voor asfalt uit metingen
- Het bepalen van de sterkte van een asfaltbekleding op basis van proefstukken
- Niet-destructief onderzoek voor laagdikte asfaltbekledingen en asfaltkwaliteit
- Bepaling laagdikte asfaltbekledingen uit grondradar
- Het bepalen van de dichtheid van een asfaltbekleding met de nucleaire dichtheidsmeter
- Testen voor mechanische eigenschappen asfalt
- Bepalen mechanische eigenschappen asfaltbekledingen uit laboratoriumonderzoek
- 4.3.1 Mechanische eigenschappen asfaltbekleding
- 4.4 Parameters grasbekleding
- 4.5 Parameters breuksteen
- 5. Rekenmodellen voor dijkerosie
- 5.1 Steenzetting
- Model beoordeling stabiliteit toplaag steenzettingen (ZST)
- Toplaaginstabiliteit onder afschuiving (ZAF)
- Toplaaginstabiliteit onder golfaanval (ZTG) - Toetsing
- Toplaaginstabiliteit onder langsstroming (ZTS)
- Materiaaltransport vanuit de ondergrond
- Invloed vlijlagen op materiaaltransport vanuit de ondergrond
- Nadere analyse van de erosie van de onderlagen (ZEO)
- 5.2 Asfalt
- Model AGK - Bezwijken van de asfaltbekleding ten gevolge van golfklappen
- Voorbeeld van een toepassing van het rekenmodel AGK
- Model ASP - Bezwijken asfaltbekleding door ontstaan S-profiel
- Model AWO - Bezwijken van de asfaltbekleding ten gevolge van wateroverdrukken
- Voorbeeld van een toepassing van het rekenmodel AWO
- Beoordeling van asfaltbekledingen op ernstige schade (AES)
- Beoordelen van materiaaltransport door het asfalt (AMT)
- 5.3 Grasbekleding
- Model GEKB - Erosie van de grasbekleding op de kruin en het binnentalud
- Model GEBU-golfklap - Erosie van de grasbekleding buitentalud door golfklappen
- Model GEBU-golfoploop - Erosie van de grasbekleding buitentalud als gevolg van golfoploop
- Model GABU - Afschuiven door stabiliteitsverlies van de grasbekleding van het buitentalud
- 5.4 Breuksteenconstructies
- 5.1 Steenzetting
- 6. Oplossingen voor dijkverbetering
- 6.1 Steenzettingen
- Voorselectie bekledingstypen
- Dimensioneringsprincipes van de filters onder een steenzetting
- Keuze soort geokunststof of granulair filter
- Standaard steenzettingen dimensionering op toplaagstabiliteit
- Verschil hergebruik en nieuw aan te voeren toplaagelementen
- Dimensioneren van nieuw aan te voeren standaardelementen op een granulaire laag
- Dimensioneren hergebruikte standaardelementen op granulaire laag
- Dimensioneren steenzettingen met afstandhouders
- Dimensioneren blokkenmatten
- Dimensioneren van doorgroeistenen
- Dimensioneren ingegoten steenzetting
- Dimensioneren steenzettingen met ruwheidselementen
- Samenstellen van dwarsprofielen van de mogelijke varianten voor de dijkbekleding
- Iteratief optimaliseren van het ontwerp van een steenzetting
- Dimensioneren berm bij steenzettingen
- Dimensioneren van de tonrondte in een steenzetting
- Maatregelen tegen afschuiving van steenzettingen
- Dimensioneren van de teenconstructie bij een steenzetting
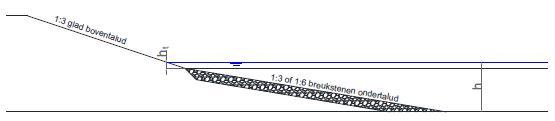
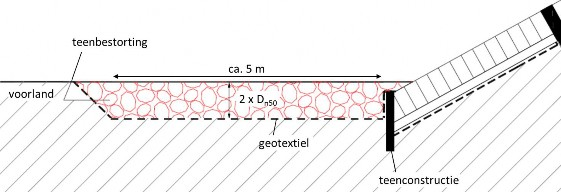
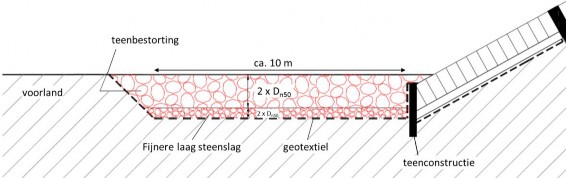
- Dimensioneren van de teenbestorting
- Dimensioneren van overgangs- en aansluitingsconstructies tussen twee bekledingstypes
- Dimensioneren type betonband bij overgangs- en aansluitingsconstructies
- Dimensioneren buitentalud in de golfoploopzone
- Dimensioneren overstroombare kruin en binnentalud
- Dimensioneren kruin boven ontwerppeil en bijbehorend binnentalud
- 6.2 Asfaltbekledingen
- 6.3 Breuksteenconstructies
- Dimensioneren van een steenbestorting
- Dimensioneren van een breuksteenbekleding op windgolven
- Dimensioneren van een breuksteenbekleding op stromingsbelasting
- Dimensioneren van een breuksteenbekleding op scheepsbelastingen
- Dimensioneren van breuksteenbekleding op ijsbelasting
- Het dimensioneren van een breuksteenoverlaging
- 6.1 Steenzettingen
- 7. Beheer
- 7.1 Algemeen
- 7.2 Beheer van bekledingen
- Beschrijving van de traditionele bekledingen
- Specifieke aandachtspunten in het ontwerp en de aanleg van dijkbekledingen
- Aandachtspunten bij de verschillende bekledingstypen
- Eisen en wensen bekledingen vanuit secundaire functies
- Methoden om sterkte aan te tonen van een nieuw type bekleding
- Constructiegerelateerde belastingen op bekledingen
- 7.3 Steenzettingen
- 7.4 Asfaltbekleding
- 7.5 Grasbekleding
- 7.6 Breuksteenconstructies
Dimensioneren van een steenbestorting
Literatuur
Capel, A. Handreiking dijkbekledingen : Deel 4 Breuksteenbekledingen – Aanvulling bij Rock Manual (HDD4). Rijkswaterstaat (RWS WVL) en Projectbureau Zeeweringen, november 2015.
Ebbens, R.E. Toe structures of rubble mound breakwater : Stability in depth limited conditions. Technische Universiteit Delft, master thesis, 2009.
The Rock Manual : The use of rock in hydraulic engineering ; Second edition. CIRIA, 2007.