- 1. Mechanismen dijkerosie
- 1.1 Fenomenologische beschrijvingen
- Fenomenologische beschrijving van het mechanisme dijkerosie
- 1.1.1. Steenzettingen
- Fenomenologische beschrijving van de stabiliteit van een steenzetting op het buitentalud
- Falen van teen-, overgangs- of aansluitingsconstructie
- Bezwijkmechanismen van aan steenzettingen verwante bekledingstypen
- Bezwijken van ingegoten steenzettingen
- Bezwijken van geschakelde steenzettingen
- Bezwijken van doorgroeistenen
- Bezwijken van steenzetting op een berm
- Bezwijken steenzettingen door niet-hydraulische beschadiging
- 1.1.2 Asfaltbekledingen
- 1.1.3 Grasbekledingen
- Fenomenologische beschrijving van de grasbekleding op het buitentalud
- Fenomenologische beschrijving van de grasbekleding op de kruin en het binnentalud
- Uittrekmechanisme bij grasbekledingen
- Schade door stromingingsconcentraties langs objecten
- Schade door stroming rond niet goed beheerbare delen
- Slijterosie van grasbekledingen
- Erosie van overgangen / discontinuïteiten in grasbekledingen
- Jet-erosie bij grasbekledingen
- Afstropen van de grasbekleding
- Headcut erosie bij grasbekledingen
- 1.1.4 Breuksteenbekleding
- 1.2 Beschrijving dijkbekledingen
- 1.2.1 Steenzettingen
- Beschrijving van de verschillende onderdelen van een steenzetting
- Functies van een steenzetting
- Varianten in steenbekledingssystemen
- Toplaag steenzetting van standaardelementen
- Toplaag steenzetting van aanverwante bekledingstypen
- Ingezande en ingeslibte toplaag van de steenzetting
- Inwasmateriaal in een steenzetting
- Granulaire laag van een steenzetting
- Granulaire aanvulling van een dijklichaam onder een steenzetting
- Geokunststof in steenzettingen
- 1.2.2. Asfaltbekledingen
- 1.2.3 Grasbekledingen
- 1.2.4 Breuksteenconstructies
- 1.2.1 Steenzettingen
- 1.1 Fenomenologische beschrijvingen
- 2. Veiligheidsanalyse dijkerosie
- 3. Belastingen
- Hydraulische belastingen op dijkbekledingen
- Belastingzones voor zee- en estuariadijken
- 3.1 Waterstanden
- 3.2 Belastingverloop
- Belastingverloop bekledingen
- Waterstandsverloop voor het mechanisme toplaaginstabiliteit van zetsteen (ZST)
- Waterstandsverloop voor het mechanisme bezwijken van de asfaltbekleding (AGK en ASP)
- Waterstandsverloop voor het mechanisme erosie van de grasbekleding op het buitentalud (GEBU oploop en golfklap)
- Belastingduur voor het mechanisme erosie van de grasbekleding op de kruin en het binnentalud (GEKB)
- 3.3 Golven
- Bepaling van de golfhoogte gegeven een overschrijdingsfrequentie
- Golfcondities per waterstandsniveau
- Golfoverslag en overloop - definities
- Golfoploop
- Effect ruwheid steenzetting op golfoploop
- Golfklappen
- Gemiddeld overslagdebiet
- Vertaling van gemiddeld golfoverslagdebiet naar golfhoogte
- Simuleren hydraulische belasting voor afschuiven grasbekleding binnentalud
- Proeven met de golfoverslagsimulator
- Golfoverslag simuleren met een golfoverslagsimulator
- Stroomsnelheid en laagdikte op de kruin bij overslag
- Verloop snelheden tijdens overslag
- Aantal golven voor ontwerp en toetsing van breuksteen
- 3.4 Overige belastingen
- 4. Karakteriseren van dijklichaam en bekledingen
- 4.1 Dijkprofiel en voorland
- 4.2 Parameters steenzetting
- 4.2.1 Toplaagelementen
- Dikte toplaagelement steenzetting
- Het bepalen van de toplaagdikte van een steenzetting
- Dichtheid toplaagelement steenzetting
- Open ruimte tussen toplaagelementen steenzetting
- Open oppervlak toplaagelementen steenzetting
- De korrelgrootte van het inwasmateriaal van een toplaagelement steenzetting
- Parameters voor bepalen toplaaginstabiliteit door langsstroming
- Parameters voor bepalen toplaaginstabiliteit door golfoploop
- 4.2.2. Granulaire laag
- Eigenschappen granulaire laag
- Materiaaleigenschappen granulaire laag onder steenzettingen
- Het bepalen van representatieve parameters voor granulaire aanvullingen in steenzettingen
- Dikte van de granulaire laag onder steenzettingen
- (Conservatieve) Standaardwaarden voor de porositeit van de granulaire laag bij steenzettingen
- 4.2.3 Geokunststof en onderlagen
- 4.2.4. Overige invloedsparameters voor stabiliteit steenzettingen
- 4.2.1 Toplaagelementen
- 4.3 Parameters asfalt
- 4.3.1 Mechanische eigenschappen asfaltbekleding
- De laagdikte van een asfaltbekleding
- Stijfheid asfaltbekleding
- Valgewicht-deflectiemeter
- De doorlatendheid van asfalt
- Sterkte asfaltbekleding
- De holle ruimte van asfaltbekleding
- De dichtheid van asfaltbekleding
- De beddingsconstante van de ondergrond bij een asfaltbekleding
- De doorlatendheid van de ondergrond te beschouwen voor opdrijven gesloten bekleding
- 4.3.2 Testen voor eigenschappen asfaltbekleding
- Bepalen karakteristieke waarden voor asfalt uit metingen
- Het bepalen van de sterkte van een asfaltbekleding op basis van proefstukken
- Niet-destructief onderzoek voor laagdikte asfaltbekledingen en asfaltkwaliteit
- Bepaling laagdikte asfaltbekledingen uit grondradar
- Het bepalen van de dichtheid van een asfaltbekleding met de nucleaire dichtheidsmeter
- Testen voor mechanische eigenschappen asfalt
- Bepalen mechanische eigenschappen asfaltbekledingen uit laboratoriumonderzoek
- 4.3.1 Mechanische eigenschappen asfaltbekleding
- 4.4 Parameters grasbekleding
- 4.5 Parameters breuksteen
- 5. Rekenmodellen voor dijkerosie
- 5.1 Steenzetting
- Model beoordeling stabiliteit toplaag steenzettingen (ZST)
- Toplaaginstabiliteit onder afschuiving (ZAF)
- Toplaaginstabiliteit onder golfaanval (ZTG) - Toetsing
- Toplaaginstabiliteit onder langsstroming (ZTS)
- Materiaaltransport vanuit de ondergrond
- Invloed vlijlagen op materiaaltransport vanuit de ondergrond
- Nadere analyse van de erosie van de onderlagen (ZEO)
- 5.2 Asfalt
- Model AGK - Bezwijken van de asfaltbekleding ten gevolge van golfklappen
- Voorbeeld van een toepassing van het rekenmodel AGK
- Model ASP - Bezwijken asfaltbekleding door ontstaan S-profiel
- Model AWO - Bezwijken van de asfaltbekleding ten gevolge van wateroverdrukken
- Voorbeeld van een toepassing van het rekenmodel AWO
- Beoordeling van asfaltbekledingen op ernstige schade (AES)
- Beoordelen van materiaaltransport door het asfalt (AMT)
- 5.3 Grasbekleding
- Model GEKB - Erosie van de grasbekleding op de kruin en het binnentalud
- Model GEBU-golfklap - Erosie van de grasbekleding buitentalud door golfklappen
- Model GEBU-golfoploop - Erosie van de grasbekleding buitentalud als gevolg van golfoploop
- Model GABU - Afschuiven door stabiliteitsverlies van de grasbekleding van het buitentalud
- 5.4 Breuksteenconstructies
- 5.1 Steenzetting
- 6. Oplossingen voor dijkverbetering
- 6.1 Steenzettingen
- Voorselectie bekledingstypen
- Dimensioneringsprincipes van de filters onder een steenzetting
- Keuze soort geokunststof of granulair filter
- Standaard steenzettingen dimensionering op toplaagstabiliteit
- Verschil hergebruik en nieuw aan te voeren toplaagelementen
- Dimensioneren van nieuw aan te voeren standaardelementen op een granulaire laag
- Dimensioneren hergebruikte standaardelementen op granulaire laag
- Dimensioneren steenzettingen met afstandhouders
- Dimensioneren blokkenmatten
- Dimensioneren van doorgroeistenen
- Dimensioneren ingegoten steenzetting
- Dimensioneren steenzettingen met ruwheidselementen
- Samenstellen van dwarsprofielen van de mogelijke varianten voor de dijkbekleding
- Iteratief optimaliseren van het ontwerp van een steenzetting
- Dimensioneren berm bij steenzettingen
- Dimensioneren van de tonrondte in een steenzetting
- Maatregelen tegen afschuiving van steenzettingen
- Dimensioneren van de teenconstructie bij een steenzetting
- Dimensioneren van de teenbestorting
- Dimensioneren van overgangs- en aansluitingsconstructies tussen twee bekledingstypes
- Dimensioneren type betonband bij overgangs- en aansluitingsconstructies
- Dimensioneren buitentalud in de golfoploopzone
- Dimensioneren overstroombare kruin en binnentalud
- Dimensioneren kruin boven ontwerppeil en bijbehorend binnentalud
- 6.2 Asfaltbekledingen
- 6.3 Breuksteenconstructies
- Dimensioneren van een steenbestorting
- Dimensioneren van een breuksteenbekleding op windgolven
- Dimensioneren van een breuksteenbekleding op stromingsbelasting
- Dimensioneren van een breuksteenbekleding op scheepsbelastingen
- Dimensioneren van breuksteenbekleding op ijsbelasting
- Het dimensioneren van een breuksteenoverlaging
- 6.1 Steenzettingen
- 7. Beheer
- 7.1 Algemeen
- 7.2 Beheer van bekledingen
- Beschrijving van de traditionele bekledingen
- Specifieke aandachtspunten in het ontwerp en de aanleg van dijkbekledingen
- Aandachtspunten bij de verschillende bekledingstypen
- Eisen en wensen bekledingen vanuit secundaire functies
- Methoden om sterkte aan te tonen van een nieuw type bekleding
- Constructiegerelateerde belastingen op bekledingen
- 7.3 Steenzettingen
- 7.4 Asfaltbekleding
- 7.5 Grasbekleding
- 7.6 Breuksteenconstructies
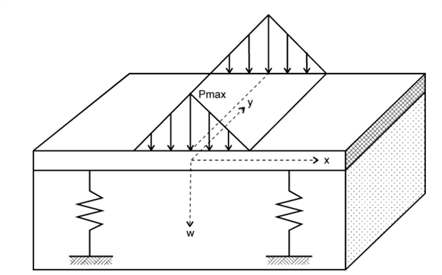
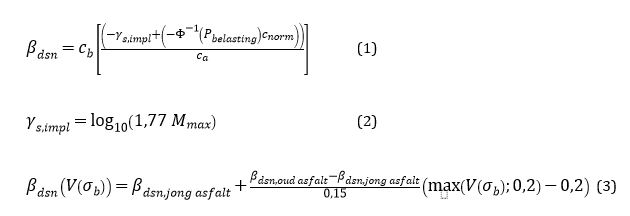
Model AGK - Bezwijken van de asfaltbekleding ten gevolge van golfklappen
Gerelateerde artikelen
- Fenomenologische beschrijving van de stabiliteit van een asfaltbekleding op het buitentalud
- Belastingverloop bekledingen
- Schematisatie van het dijkprofiel voor de analyse van een asfaltbekleding
- De laagdikte van een asfaltbekleding
- Stijfheid asfaltbekleding
- De beddingsconstante van de ondergrond bij een asfaltbekleding
- Sterkte asfaltbekleding
- Waterstandsverloop voor het mechanisme bezwijken van de asfaltbekleding (AGK en ASP)
- Golfcondities per waterstandsniveau
Literatuur
De Looff, A.K., R. 't Hart, C.C. Montauban en M.F.C. van de Ven. Golfklap A Model To Determine The Impact Of Waves On Dike Structures With An Asphaltic Concrete Layer. 30th International Conference on Coastal Engineering, San Diego, september 2006.
Klerk, W.J. en W. Kanning. Calibration of Safety Factors for wave impact on Hydraulic Asphalt Concrete Revetments ; WTI cluster C. Deltares, rapport 1209431-01 0-ZWS-0002, december 2014.