Het aangepaste rekenmodel van Sellmeijer vervolg - Rekenmodellen en rekenregels

Uit eerdere pipinganalyses is gebleken dat de doorlatendheid van het zandpakket van belangrijke invloed is op het pipingmechanisme. Omdat de doorlatendheid vaak onbekend is, wordt voor de toetsing veelvuldig gebruik gemaakt van schattingen van de doorlatendheid., ontleent aan TNO-grondwaterkaarten of ontleend aan relaties met de korrelverdeling. Schattingen op basis van grondwaterkaarten kunnen soms conservatief zijn omdat hier vaak de diepere grovere en dus doorlatendere zandlagen dominant zijn.

De relatie met korrelgrootteverdeling zou wel eens optimistisch kunnen zijn omdat deze over het algemeen gebaseerd is op korrelgrootteverdelingen van zandmonsters die gewonnen zijn in de top van de zandlaag, die meestal fijner is en dus ondoorlatender dan de diepere zandlagen.

In het rekenmodel is in de sterktefactor ook een term opgenomen voor de relatieve dichtheid. De aangepaste rekenregel is alleen voor een relatieve dichtheid van groter dan 50% gevalideerd. De invloed van de relatieve dichtheid lijkt niet zo dominant dat het de moeite loont om voor de toetsing deze parameter extra te bepalen. Het wordt daarom aangenomen

4. Met REGIS II (REgionaal Geohydrologisch InformatieSysteem) hebben landelijke en regionale overheden, waterbeheerders, adviesbureaus en opleidingscentra gratis en online de beschikking over een hydrogeologisch ondergrondmodel van Nederland. REGIS II geeft, door middel van digitale kaartbestanden, inzicht in de hydrogeologische opbouw en doorlatendheid van de ondergrond op een regionale schaal. Daarnaast vormt REGIS II een adequate basis voor ondergrondschematisaties ten behoeve van landelijke en regionale grondwatermodellen. Aangevuld met lokale (boor)informatie is REGIS II ook een uitgangspunt voor lokale grondwatermodellen. Iedereen heeft via DINOLoket, de centrale toegangspoort tot Data en Informatie van de Nederlandse Ondergrond, gratis toegang tot de gegevens van REGIS II.

dat de relatieve dichtheid bij RD > 50 % bijna geen invloed op het kritieke verval heeft. Dit is een veilige ondergrens. In de toetsregel zelf (zie hoofdstuk 7) is de relatieve dichtheid niet als parameter meegenomen omdat ten eerste de relatieve dichtheid in de praktijk moeilijk te meten is en ten tweede de onzekerheid rondom de invloed van de relatieve dichtheid klein is ten opzichte van de totale onzekerheid van de rekenregel. De invloed van de relatieve dichtheid is in de toetsregel meegenomen in de modelonzekerheid [Lopez de la Cruz et al., 2010].

Opgemerkt wordt dat onderscheid wordt gemaakt tussen pure rekenmodel/rekenregel en toetsregel voor piping. Het rekenmodel beschrijft de fysica van het pipingmechanisme. De toetsregel betreft de receptuur voor het gebruik van de rekenregel bij de toets op veiligheid. De toetsregel omvat daar omheen ook nog een veiligheidsfilosofie, zoals die in hoofdstuk 10 is toegelicht, is ontwikkeld. De toetsregel en het toetsvoorschrift voor de gedetailleerde toetsing zijn in hoofdstuk 7 omschreven.

De aanpassing van de rekenregel is geldig voor in Nederland voorkomende zanden. Ter afbakening van het geldigheidsgebied zijn proeven ook op medium schaal uitgevoerd. Voor grove zanden (d70= 500 µm) lijkt het aangepaste model een betere afschatting te geven van het kritiek verval dan het oude model. Voor fijnere zanden is het verschil tussen oude en nieuwe model minder sterk.

Tot nader inzicht is het aangepaste model een veilige benadering voor het schatten van het kritiek verval. Het geldigheidsgebied is gevalideerd van een d70 van 150 μm (kleinste d70 toegepast bij kleine schaalproeven) tot een d70 van 500 μm.

In [TAW, 1994] zijn praktische aanbevelingen op basis van de formule van Sellmeijer ontwikkeld ten aanzien van de wijze waarop onzekerheden in de parameterkeuzen kunnen worden verdisconteerd. In Tabel 5.2 is de aanbevolen keuze van de representatieve parameters samengevat.

De parameters d70en k (=*g/) dienen onafhankelijk van elkaar te worden beschouwd. Het wordt daarom aanbevolen de doorlatendheid op basis van pompproeven of uit REGIS II te nemen, omdat de toestroming meestal niet wordt bepaald door een lokaal gevonden zandsoort, maar door de dikke Pleistocene zandpakketten in de ondergrond. De d70 van de bovenste pipinggevoelige laag is bepalend voor het loskomen van de zandkorrels.

De nominaal vastgestelde waarden in deze tabel kunnen niet op eenvoudige wijze van geval tot geval worden bepaald. Bovendien wordt door deze vaststelling de modelfout in het oorspronkelijke model van Sellmeijer afgedekt.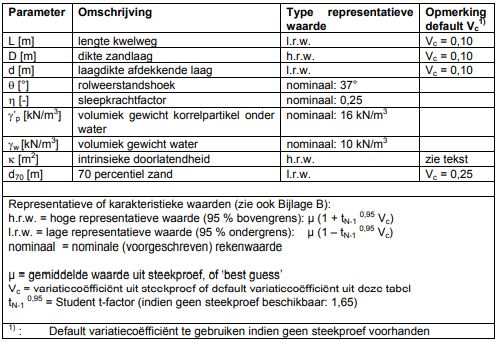

Tabel 5.2 Representatieve parameterkeuze bij ontwerp/toetsing bij gebruik van de formule van Sellmeijer

Sellmeijer in tweelagensysteem

Het rekenmodel van Sellmeijer is afgeleid voor een analytische oplossing van een standaardgeometrie met een geïdealiseerde bodemsamenstelling, dat wil zeggen een homogene horizontale watervoerende zandlaag met één uniforme (en isotrope) doorlatendheid en met een constante dikte die zich uitstrekt tot voorbij het uittreepunt, afgedekt door een compleet ondoorlatende waterkering en niet onderbroken door kwelschermen en dergelijke. In de praktijk zijn watervoerende zandpakketten vaak niet uniform van samenstelling, maar kunnen laagsgewijs bestaan uit zanden met verschillende fijnheden en doorlatendheden. Het watervoerende pakket kan bijvoorbeeld bestaan uit een laag fijn holoceen dekzand op de doorgaans grovere pleistocene zandlaag. Dit betekent dat de doorlatendheid zich niet goed door één doorlatendheidscoëfficiënt laat karakteriseren, wat het toepassen van de rekenregel van Sellmeijer bemoeilijkt. Het model is echter toch toepasbaar mits het product van laagdikte en doorlatendheid van het zandpakket in het model zo gekozen wordt, dat de kwelstroming in de prototypesituatie wordt gesimuleerd.

Voor een zorgvuldige toetsing is het daarom belangrijk om ook dijken te kunnen beoordelen met afwijkende condities. Binnen het project Veiligheid Nederland in Kaart (VNKI & II) is gewerkt aan een rekenmodel waarbij de watervoerende zandlaag willekeurig gemodelleerd kan worden als samenstel van volumes zand met verschillende doorlatendheden. De berekening van het kritieke verval kan hier alleen via een numerieke benadering worden uitgevoerd. De stationaire oplossing van het stromingsveld is geïmplementeerd in het computerprogramma voor numerieke grondwaterstromingsanalyse MSeep, dat is gebaseerd op een Eindige Elementen Methode. Het erosiekanaal wordt hier gemodelleerd als een

speciale randvoorwaarde waarmee het stijghoogteverschil bij gegeven erosielengte vervolgens stapsgewijs wordt bepaald.

Voor het verloop van de stijghoogte in het erosiekanaal wordt een aanname gedaan, vervolgens wordt getoetst in hoeverre voldaan wordt aan de evenwichtscondities van zandkorrel in het erosiekanaal. Met de uitbreiding van MSeep voor een pipinganalyse kunnen de effecten van een niet homogene opbouw van de pipinggevoelige watervoerende zandlaag worden meegenomen. Ten opzichte van de rekenregel van Sellmeijer biedt dit het voordeel dat de watervoerende zandlaag niet eerst moeizaam als één homogene laag moet worden geschematiseerd.

In [Knoeff, 2009] wordt de achtergrond van MSeep beschreven. Daarbij wordt speciaal stilgestaan bij de consequenties van de nieuwe inzichten uit SBW Hervalidatie Piping voor MSeep en de aanpassingen die daardoor aan het programma zijn gedaan.

Door de commissie Vrijling is naar aanleiding van de hoge faalkansen voor piping in het project VNK een studie opgeleverd [Thonus et al., 2005] waarin onder andere is gekeken naar de invloed van het meenemen van meerdere lagen met een verschillende doorlatendheid. In deze studie is aan de hand van MSeep berekeningen aangetoond dat het rekenen met een 2-lagensysteem met verschillende doorlatendheden leidt tot een betrouwbaarder resultaat. Verder is in deze studie een methode gegeven om vanuit een 2- lagen modellering te komen tot een 1-laags modellering voor de rekenregel van Sellmeijer.

In een andere studie [Duinen, 2005] is onderzoek gedaan naar de gevoeligheid van de modellering (laagopbouw) en parameterkeuze. Hier is aangetoond dat de verschillende methoden die beschikbaar zijn om de doorlatendheid van een zandpakket te bepalen verschillende resultaten geven. Afhankelijk van de gekozen methode levert dit dus een bepaald resultaat in de pipinganalyse.

Uit analyses met het numerieke grondwaterstromingsmodel MSeep met pipingmodule is vastgesteld dat het tot een betrouwbaarder resultaat leidt als in de schematisatie van de ondergrond met verschillen in doorlatendheden wordt rekening gehouden. Het rekenen met een meer-lagen systeem in MSeep levert een realistischer kritiek verval dan bij het rekenen met een één-laag systeem [Blinde, 2009].

Als met de rekenregel van Sellmeijer wordt gewerkt zal een equivalente doorlatendheid moeten worden bepaald, die het meer-lagen systeem representeert. Schematisatie keuzes in het numerieke model zoals de grootte van de meshelementen hebben effect op het berekende verval.

Voor het project VNK-II is met behulp van het rekenmodel MSeep een specifieke applicatie voor pipinganalyse ontwikkeld, waarbij het watervoerende pakket uit twee horizontale zandlagen kan worden opgebouwd (zie Figuur 5.6). Deze applicatie, genaamd MPiping-VNK, is een artificieel neuraal netwerk (ANN), waarmee het kritieke verval berekend kan worden als functie van de verschillende doorlatendheden van deellagen waaruit het watervoerende pakket is opgebouwd, inclusief een deellaag die de bedding van de rivier representeert en de korrelgrootte karakteristieken van de bovenste deellaag.

Dit ANN is getraind en afgeregeld aan de hand van grote aantallen numerieke berekeningen met de pipingmodule in MSeep. Voordeel van het ANN is dat hiermee heel snel kritieke vervallen kunnen worden berekend. Dit ANN is als een module gekoppeld aan PC-Ring (in detoekomst genoemd ‘Hydra-Ring’), waardoor het mogelijk is om faalkansen als gevolg van piping in een tweelaag systeem te berekenen zonder toename van benodigde rekentijden.

De nodige ondergrondgegevens die de invoer vormen van de rekenregel van Sellmeijer worden uit de DINO-database onttrokken en waar relevant door locale gegevens aangevuld.

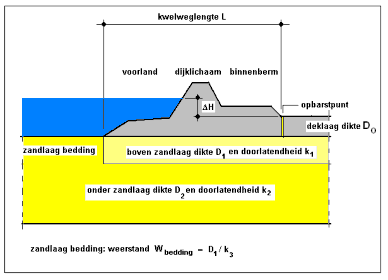
Figuur 5.6 Configuratie van deellagen van het watervoerende pakket waarvoor een ANN is ontwikkeld t.b.v. berekeningen met MPiping-VNK in PC-Ring