Eisen aan dichte erosiewerende filters
Voor dichte erosiewerende filters zijn volgende eisen belangrijk:
- interne stabiliteit, dat wil zeggen het filtermateriaal zelf mag niet gaan bewegen;
- externe stabiliteit, dat wil zeggen voorkomen moet worden dat gronddeeltjes door het filtermateriaal heen worden getransporteerd;
- waterdoorlatendheid
De klassieke formules voor dichte filters zijn er op gericht aan deze eisen tegemoet te komen. Essentieel daarbij is de grootte van het poriënkanaaltje in het filtermateriaal. Een poriënkanaaltje is de verbinding tussen de afzonderlijke holtes tussen de poriën. Per definitie zijn poriënholtes de grootste gaten in een filter, maar voor erosie van materiaal zijn de poriënkanaaltjes relevant, en niet de poriënholtes.
De poriënkanaaltjes, in het Engels “constrictions” genoemd, zijn afhankelijk van de pakking en van de korrelverdeling. De diameter Dc van de poriënkanaaltjes varieert bij een homogeen filter tussen 0,155 en 0,414 keer de diameter. Bij een gegradeerd filter hangt de waarde van Dc af van de verhoudingen tussen de grootste korrels en de gemiddelde korreldiameter en de kleinste korrels en de gemiddelde korreldiameter.
Interne stabiliteit
Transport van filtermateriaal is niet wenselijk. Transport ontstaat in filtermateriaal dat intern instabiel is door een gap-graded zeefkromme of een brede gradering. Interne stabiliteit treedt theoretisch niet op als geldt df60 / df10 < 6. Een hierop gebaseerd praktisch criterium is [Pilarczyk, 1998]:
d60 / d10 < 10 (8.1)
Overigens leidt interne erosie tot compactie en zal niet zo snel tot schade aan de constructie leiden.
Naast formule (8.1) bestaat er ook een alternatieve formulering die rekening houdt met de zeefkromme van het filtermateriaal:
d10 < 4d5 (8.2)
d20 < 4d10
d30 < 4d15
d40 < 4d20
Heibaum [2004] presenteert een grafiek die in Duitsland wordt gebruikt voor het ontwerpen van granulaire filters. De methode is bruikbaar voor standaard graderingen en voor breed-gegradeerde graderingen.
Externe stabiliteit
Op basis van onderzoek is een relatie afgeleid voor de grootte van een poriënkanaaltje in granulair materiaal als functie van een kenmerkende diameter. Dit kan worden vertaald naar de fundamentele filterregel voor dichte filters:
d f 15 / db85 < 5 (of voor uniform gegradeerde filters d f 50 / db50 < 10 ) (8.3)
waarin:
df15 is de diameter van het filtermateriaal waarvan 15% van de deeltjes kleiner is dan df15, db85 is de diameter van de gronddeeltjes waarvan 85% van de diameter van gronddeeltjes kleiner is dan db85, en df50 en db50 zijn de gemiddelde diameters van filter en grondmateriaal.
Bij breed gegradeerd filtermateriaal neemt de diameter van het maatgevende poriëkanaaltje af en is deze niet langer een functie van df15 maar van een kleinere diameter. De relatie is dan onnodig veilig.
Overigens is er sprake van breed gegradeerd materiaal als geldt d85/d15 > 2,5. Dit is conform de [NEN-EN-13383]. Voor de volledigheid wordt opgemerkt dat in de Rock Manual [CUR/CIRA/CETMEF, 2007] een factor 1,5 wordt aangehouden als onderscheid tussen breed gegradeerd en standaard gradering.
Bij gegradeerde grond neemt de kans toe dat een gronddeeltje veel kleiner is dan het poriënkanaaltje in het filtermateriaal. De formule is dan niet altijd veilig. Er moet dan rekening worden gehouden met het type zeefkromme: lineaire (maar zeer flauw), gap-graded, of intern instabiel. Bij de laatste twee bestaat ook het gevaar van dichtslibben van het filter.
De volgende regels als functie van de zeefkromme zijn te noemen:
- Lineaire zeefkromme waarbij log(d10/d0) - log(d20/d10) - log(d30/d20) - et cetera, of log(d10/d0) < log(d20/d10) < log(d30/d20) < et cetera. Geometrisch dicht als dc/db50 < 1.
- Gap-graded zeefkromme, waarbij er midden in de zeefkromme een bijna horizontaal deel zit, omdat het gaat om een mengsel van een fijn materiaal met een grof materiaal. Geometrisch dicht als dc/dbg < 1, waarbij dbg de d85 is van het fijne materiaal. Dus als het mengsel bestaat uit 40% fijn en 60% grof materiaal, dan geldt: dbg = db34 van het mengsel omdat 0,44 keer 85% = 34%.
- Intern instabiele “concave zeefkromme” waarbij log(d10/d0) > log(d20/d10) > log(d30/d20) > et cetera. Geometrisch dicht als dc/db30 < 1.
Voor specifieke regels voor breed-gegradeerde grond wordt naar CUR rapport 161 [CUR, 1993] verwezen.
Waterdoorlatendheid
Het filter moet voldoende waterdoorlatend zijn om te voorkomen dat zich onder het filter een waterdruk kan opbouwen. In dat geval zou namelijk het filter kunnen opbarsten, waardoor een kwelweg langs het filter kan ontstaan.
Onderscheid moet worden gemaakt in waterdoorlatendheid in loodrechte richting door het filter, relevant bij erosiewerende filters, en waterdoorlatendheid in het vlak van het filter, relevant bij filters waar de waterafvoer een belangrijke rol speelt. In algemene zin geldt dat hoe fijner het materiaal is, des te kleiner de doorlatendheid.
Voor loodrechte waterdoorlatendheid geldt de algemene regel:
d f 15 / db15 > 5 (8.4)
In veel gevallen is deze eis te streng, want hij komt overeen met een verhouding tussen loodrechte filterdoorlatendheid kf en loodrechte doorlatendheid basismateriaal kb van ongeveer 15 à 25 [CUR/CIRA/CETMEF, 2007]. Meestal is een verhouding van kf > kb voldoende, en dit betekent:
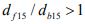 (8.5)
(8.5)
Het criterium kan nog verder worden versoepeld door gebruik te maken van de permittiviteit, gedefinieerd als Ψ = vf / H (vf = filtersnelheid (m/s); H = verval over het filter (m)), maar dan gaat ook de hydraulische belasting een rol spelen.
Opgemerkt wordt dat de waterdoorlatendheid in de loop van de tijd kan afnemen als de fijne deeltjes van het grondmateriaal worden getransporteerd en het filter verstoppen. Dit speelt vooral als er sprake is van breed-gegradeerd materiaal.
Bij de waterdoorlatendheid in het vlak van het filter is het juist de bedoeling om voldoende afvoercapaciteit te realiseren. Het verval over het filter speelt dan een rol alsmede de transmissiviteit gedefinieerd als het product van de dikte van het filter en de doorlatendheid in evenwijdige richting.
Opgemerkt wordt dat de waterdoorlatendheid in de loop van de tijd kan afnemen als de fijne deeltjes van het grondmateriaal worden getransporteerd. Het filter zal in het algemeen langzaam dichtslibben met organisch of anorganisch materiaal, of door organische activiteiten in het filter. Dit speelt vooral als er sprake is van breed-gegradeerd materiaal.
Een regelmatige controle is daarom nodig. Er is weinig ervaring met de controle van filters. Gedacht kan worden aan:
- plaatsen van peilbuizen direct onder het filter;
- visuele controle, waarbij het gehele filter wordt betrokken;
- in situ testing.
Bij het opstellen van het ontwerp dient terdege rekening te worden gehouden met de mogelijkheden tot controle.
Opbarsten
Opbarsten (of “heave”) moet worden voorkomen en dat houdt in dat het gewicht van de filterconstructie voldoende moet zijn. De eis hiervoor kan worden gerelateerd aan de verticale gradiënt i en luidt [CUR/CIRA/CETMEF, 2007]:
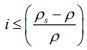 (8.6)
(8.6)
Waarin: ρs = dichtheid filtermateriaal (kg/m3 ) en ρ = dichtheid water (kg/m3 ). De waarde van de verticale gradiënt i kan worden berekend met: i = H / d met H = verval over het filter (m) en d = filterlaag dikte (m). Overigens is de eerder genoemde permittiviteit Ψ gerelateerd aan i, want met vf = k.i is af te leiden: i = Ψ.H / k
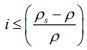 (8.6)
(8.6)