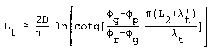Copy of Opdrijflengte bij niet-stationaire stroming (bij par. 2.3.7) - Bijlage 4

Opdrijflengte bij niet-stationaire stroming (bij par. 2.3.7)

Het opdrijfmechanisme is in wezen niet-lineair. De randvoorwaarde (de opdrijfzone) verandert afhankelijk van de grote van de belasting (geometrische niet-lineariteit). Het is daarom niet mogelijk gebruik te maken van lineaire technieken om bijvoorbeeld tijdsafhankelijke situaties te berekenen. Superpositie kan in principe niet.

Bij de aanvang van een tijdsafhankelijke situatie dient het initiële stromingsbeeld bekend te zijn en bij de uiteindelijke beschouwing te worden betrokken.

Tot het moment dat opdrijven gaat plaatsvinden is het stromingsbeeld echter wel lineair en kan gebruik gemaakt worden van lineaire transformatie-technieken, waarin de consolidatie in de toplaag in rekening kan worden gebracht. Dit is zinvol, aangezien de tijdsduur van de hoogwaterbelasting, waarbij opdrijven kan gaan plaatsvinden, gewoonlijk beperkt is. Een stationaire toestand doet zich, afhankelijk van de hydrodynamische periode van de afdeklaag, meestal veel later voor dan de duur van het hoogwater.

In de eindsituatie, als de stroming stationair is, is de opdrijflengte eenvoudig te bepalen (zie voorgaande deel).

Door Barends is in Opdrijven van ’t achterland bij hoogwater [GeoDelft, 1988] uiteengezet, dat voor de tijdsafhankelijke groei van de opdrijflengte gedurende een plots constant hoogwater de methode van de tijdsafhankelijke lekfactor gerechtvaardigd is. Voor andere tijdsafhankelijke variaties van hoogwater is er geen geschikte eenvoudige methode.

De methode van de tijdsafhankelijke lekfactor leidt tot de volgende regels:

• Het hoogwater wordt zo goed mogelijk geschematiseerd tot een sprong. Het tijdstip van de sprong wordt als begintijd: t=0 beschouwd. De hoogte van de sprong wordt aangeduid met ϕr.

• Voor de grenspotentiaal wordt de potentiaal gekozen die, gesuperponeerd op de initiële situatie, leidt tot

  opdrijven.

• Het moment van opdrijven ter plaatse van de binnenteen van de dijk treedt op als de waarde van de tijdsafhankelijke lekfactoren zodanig zijn geworden dat de kritieke potentiaal ϕkgelijk wordt aan de actuele rivierstand ϕr,

  

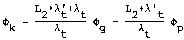
  waarin voor de tijdsafhankelijke lekfactoren geldt:

  

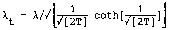
  met T = t/t en t = d2/c

  

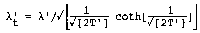
  met T’ = t/t ’ en t ’ = d’2/c’

  Voor cvmoet de “consolidatiecoëfficiënt bij zwel” worden ingevoerd (consolidatiecoëfficiënt bij ontlasten). Door  ϕk als functie van de tijd te berekenen is vast te stellen welke waarde actueel is voor de gestelde hoogwatersprong. Op dat tijdstip tkwaarop ϕkgelijk is aan de hoogwatersprong begint de opdrijfzone zich te ontwikkelen.

• Het verloop van de groei van de opdrijflengte Ltmet de tijd kan worden weergegeven door gebruik te maken van de eenvoudige formule met de tijdsafhankelijke lekfactoren:

  

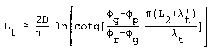
  Voor de volgende situatie is de groei van de opdrijfzone uitgewerkt.

  

  De uitwerking is gegeven in tabel b4.2.

  

  Tabel b4.2 Tijdsafhankelijke opdrijflengte

  Na ongeveer 2 uur en een kwartier zal de opdrijfzone zich gaan ontwikkelen, in het begin snel, later langzaam. In dit voorbeeld is een tijdsafhankelijke analyse zinvol als de duur van het geschematiseerd hoogwater kleiner is dan een dag.